分位点回帰は、普通の直線回帰とは少し変わった、特殊な回帰ですが、正規分布に従わないデータを処理する際、柔軟な予測をすることができる便利なモデルです。今回は、理論編・実践編に分けて、分位点回帰を解説していきたいと思います。

理論編

1.回帰

回帰とはデータ処理の方法の一つで、簡単に言うとデータを予測するモデルを作る際に、「モデル化＝簡略化」に伴う損失を最小限にすることです。そしてこの「損失」を定量化するためにモデルごとに様々な「損失関数」を定義します。「損失関数」の値を最小化するようなパラメーターを探すことが、いわゆる「学習」と呼ばれる作業になります。数多くある回帰ですが、その一つが今回紹介する「分位点回帰」です。

2.分位点

分位点回帰はその名の通り、「分位点」に注目した回帰です。「分位」とはデータを順番に並べた時に、上位何％に入るかを表現するときに使います。例えばquartileとは四分位のことで、データを四等分にできます。

0th quartile = 上位0%

1st quartile = 上位25%

2nd quartile = 上位50%

3rd quartile = 上位75%

4th quartile = 上位100%

他にもquintile=五分位など、何等分にデータを切るかは自由に設定することができます。

こういうふうにデータを区切ると、例えば身長が上位25%の人と身長が上位75%の人で変数の影響が違う場合、それらを具体的に見ることができます。これは分位点回帰が一般的な直線回帰や重回帰とは違う点です。

3.損失関数

分位点回帰の損失関数と、一般的な最小二乗法の損失関数とでは決定的な違いがあります。最小二乗法では全てのデータポイントにおける損失が均等に評価されるため、平均に対して回帰していくことになります。しかし、事故率や年収など、偏りがあるデータでは、平均における情報よりも中央値における情報の方が重要だったりします。そのため、分位点回帰などは「上位何％における変数の影響」という平均とは全く違う観点でデータを見ることができます。

「上位何％における変数の影響」を見るからといって、その上位何％のデータのみを使うわけではありません。データは常に全て使うのですが、データによって損失関数に対する影響が違う、というふうに捉えるとわかりやすいでしょうか。この損失関数を使うと、損失関数の微分が０＜＝損失関数が最小の時、上位τ％の値について予測できるような変数の係数が計算されているのです。

（もっと知りたい人向け）

具体的には損失関数は

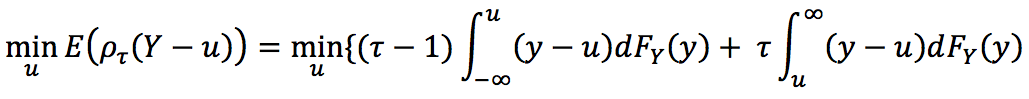
で定義されます。 ここで

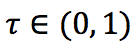
がquantileにあたる数字になります。

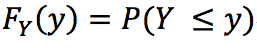
は累積分布です。

この損失関数が何故うまくいくかというと、左辺を微分したものの値が0となるような u = q_τに対して、

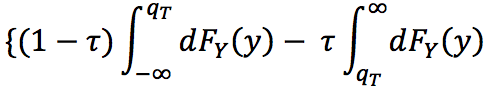
となり、整理すると

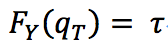
なので、確かにq_τが上位t%の値だとわかります。

4.長所と短所

上でも説明したように、分位点回帰は偏りのあるデータを処理したり、特定の分位における変数の影響を予測するのに適しています。逆に、分布が正規分布に近い場合は、平均で回帰した方が正確な結果が出ることになります。

実践編

では実際のデータを使ってQuantile Regressionを試してみましょう。今回はMicrosoft Azure MLに実装されているものを使って、飛行機の遅延について予測するモデルを訓練していきましょう。

0.データ

今回のデータは飛行機の離着陸の遅延時間、空港、日時などをまとめたデータセットです。

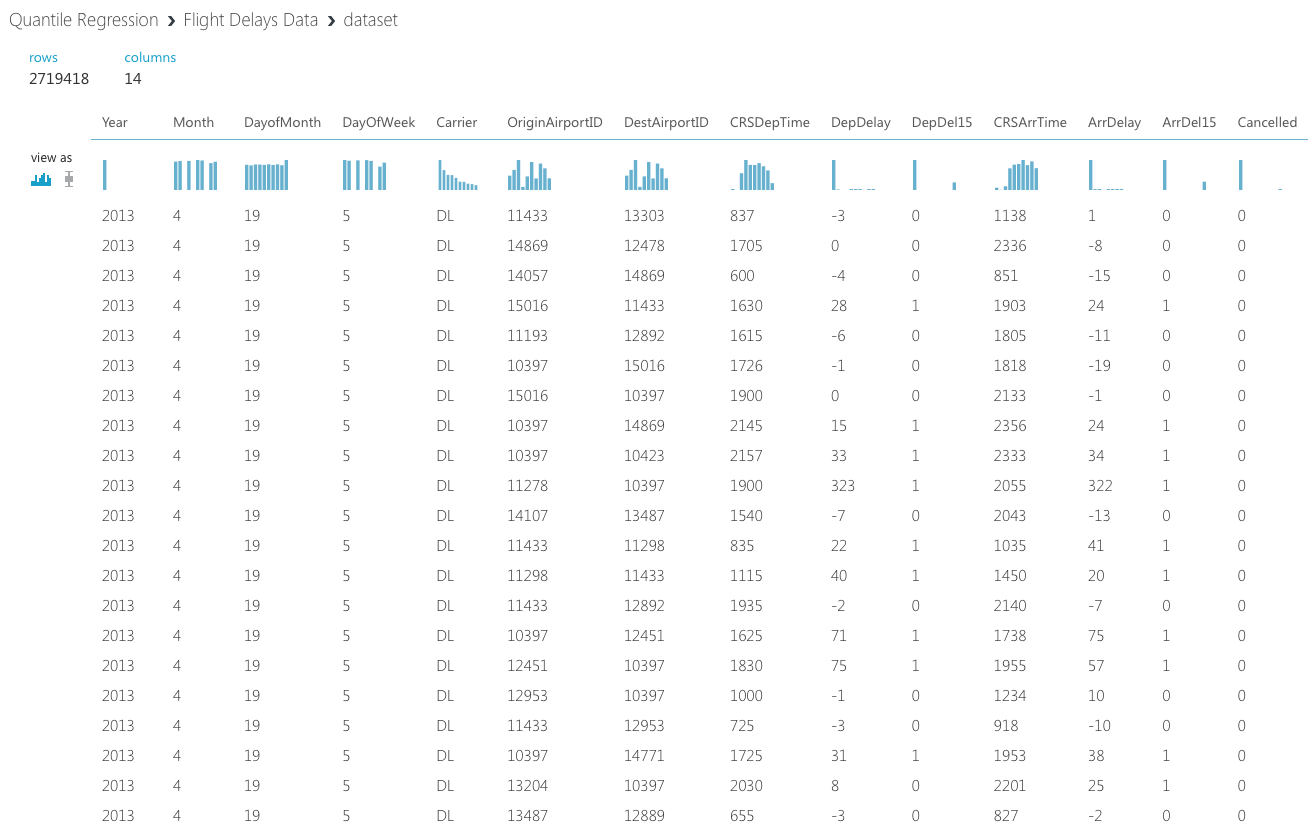
DerDelay, ArrDelayを見てみると、かなり左側に偏っていることがわかります。またCarrier（飛行機会社）も正規分布よりかなり偏っているので、Quantile Regressionを活かせそうだ、ということがわかります。通常は空白のセルの処理やデータの取捨選択が必要になりますが、今回はMicrosoft Azureに内装されたデータセットを使うので、その必要はなさそうです。

1.データの分割

学習をするにあたって、機械を学習させるための学習データ(training data)と、その学習を評価するデータ(evaluation data)の２種類が必要になってきます。そこで、元のデータをランダムに分割する"Split Data"を使います。今回は元データの60%を学習データに使用することにしました。もちろん、この値は調節可能です。

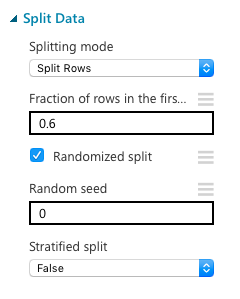
2 モデルの選択

今回はQuantile Modelを使ってみたいので、その一つであるFast Forest Quantile Regressionを使います。

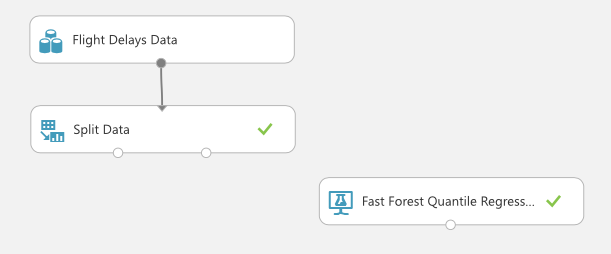
Fast Forest Quantile Regressionのパラメータは初期設定のままにしました。一部TreeやLeavesのような見慣れない単語が出てきますが、興味のある方はRandom Forest Regressionについての記事をご覧ください。

理論編で紹介した部分に当たるのは、下から２番目の"Quantiles to be estimated"になります。入力されている値を見ると、四分位なことがわかります。

3.学習

実際の学習モジュールを追加していきます。ここでは、"Train Model"モジュールに対して、どの変数を予測したいか、を指定しなければなりません。今回は出発の遅延を調べたいので、DepDelayを選びます。

また、分割したデータのうち、学習用のデータ（左側）を入力として指定します。

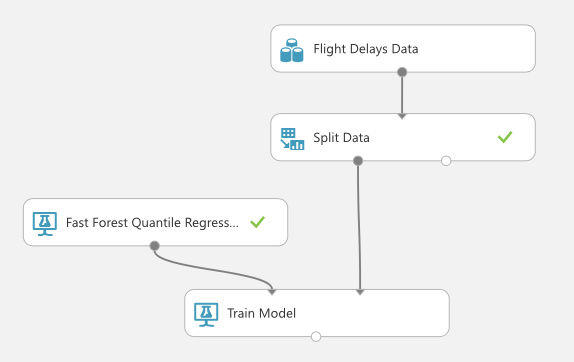
4.評価と結果

学習が終わったら、モデルの精度を「見たこともないデータをどれだけ正確に予測できたか」という基準で測ります。ここで最初に分割しておいた評価データを使うことになります。

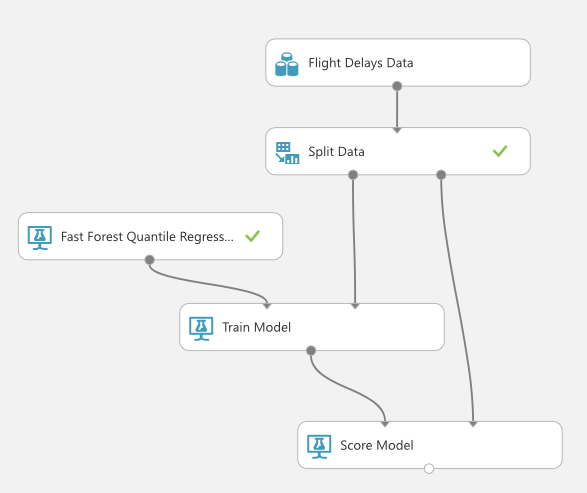
学習結果を見てみましょう。

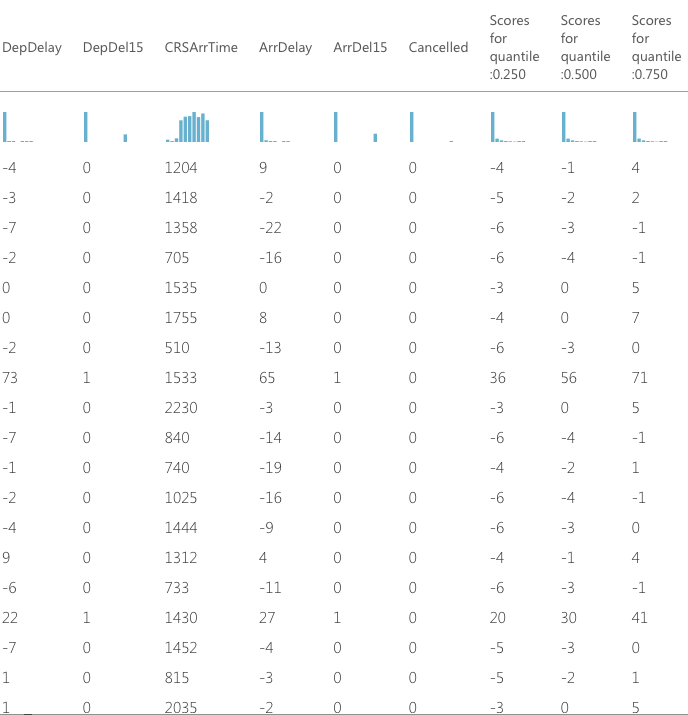
一番左端が今回予測したDepDelayで、右側3列がQuantile Regressionで予測した結果になります。

例えば一番上のDepDelay=-4のデータでは、全体の中で第１四分位に属しているため、"Score for quantile 0.250"の値が一番正確です。

逆に、中ほどにあるDepdelay=65のデータは、全体の中で第４四分位に属しているため、"Score for quantile 0.750"の値が一番正確です。

この結果からわかることの一つは、全体の中でどの四分位に属しているかによって、変数の影響が違う、ということです。でなければ、どの予想も同じような数字を出力するはずです。このような柔軟性のある分析ができるところが、分位点回帰の利点になります。

以上、分位点回帰の理論と実践でした。
その他のMicrosoft Azure Machine Learning Studioでやってみた記事も参考にしてください！
決定木アルゴリズムCARTを用いた性能評価
ロジスティクス回帰を用いた Iris Two Class Dataの分類
パラメーターチューニングを行う
ランダムフォレスト回帰を用いた人気ブログタイトル予測

参考文献： 分位点回帰を使って、「その回帰予測どれくらい外れるの?」を説明する