ここでは今は去りしデータマイニングブームで頻繁に活用されていた決定木について説明する。理論的な側面もするが、概念は理解しやすい部類であるので参考にしていただければと思う。

1 決定木(Decision Tree)

決定木とは木構造を用いて分類や回帰を行う機械学習の手法の一つで段階的にある事項のデータを分析、分離することで、目標値に関する推定結果を返すという方式である。データが木構造のように分岐している出力結果の様子から「決定木」との由来である。用途としては「意思決定のためのデータモデリング」「機械学習としての予測への活用」が挙げられる。

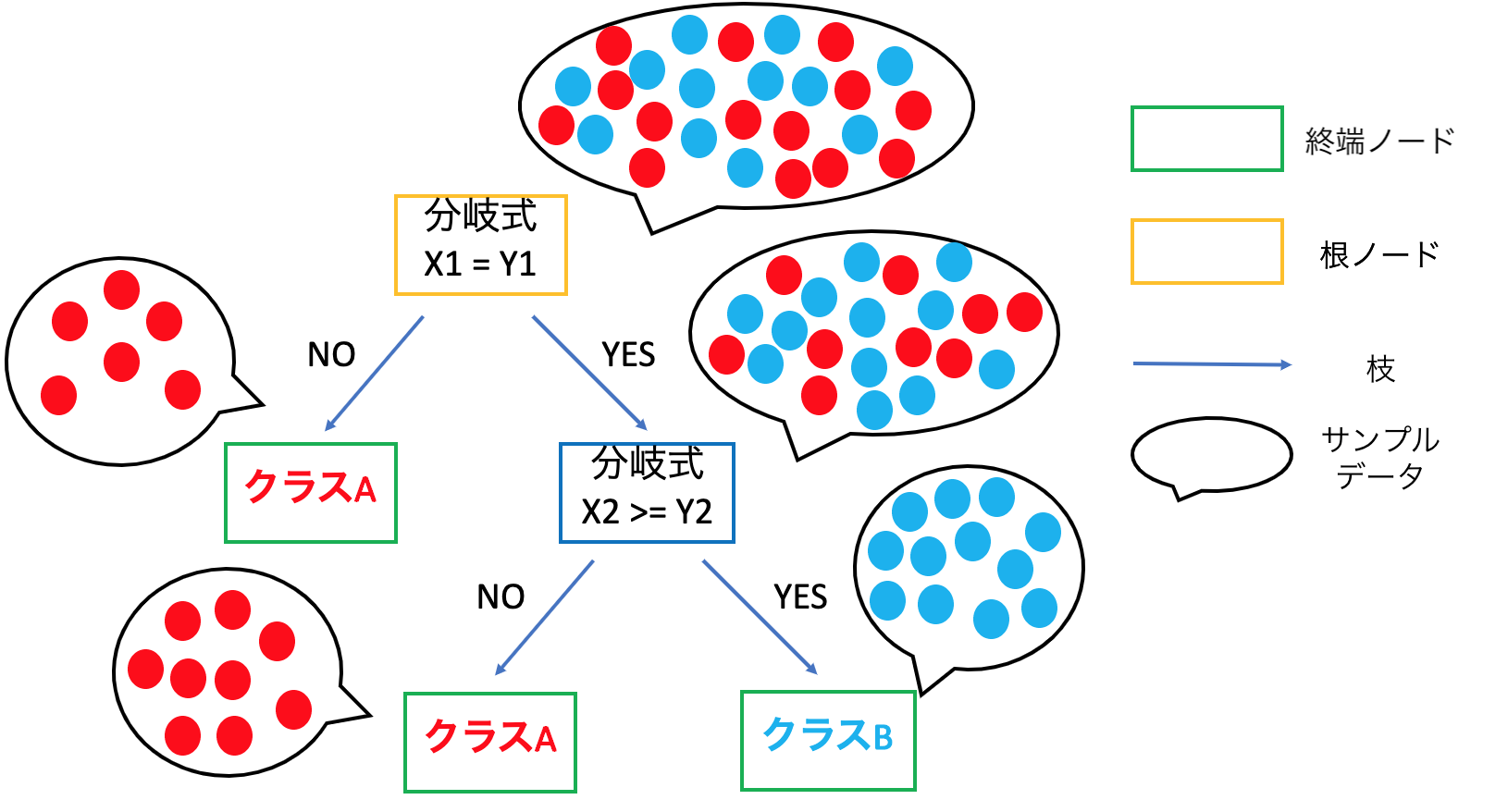
また、決定木の構成方法には、ボトムアップ的な方法とトップダウン的な方法の２種類がある。前者はある学習データを正しく判別するための識別ルール（条件式）を作成してその制約を緩めながら他の学習データも正しく判別するためのルールを汎化していく方法である。一方で後者は根ノードでできるだけ誤りの少ないように分割するルールを求めて、その後のノードでも同様に２分割するルールを次々と求めていき成長させる方法であり、分割統治法と呼ばれる。ここでは主流となっているトップダウン的な方法について記載していく。

トップダウン的な方法で決定木を構成するためには、次の要素について考える必要がある

1. 各ノードにおける特徴軸と閾値の選択
2. 終端ノードの決定(学習データがすべて分割されるかその前に止めるのか、また木の選定を行う)
3. 終端ノードに対する多数決でのクラスの割り当て

ここでトップダウン的な方法で学習する代表的な方式は３つあり（CART、ID３、C4.5）、中でも今回説明するCARTは以下の２つに大別される。

• 分類木(Classification Tree)→対象を分類する問題を解く（分類カテゴリーは２つ）（例:性別（男／女）、試合の結果（勝ち／負け）の判別）
• 回帰木(Regression Tree)→対象の数値を推定する問題を解く（例: 住宅の価格の見積り、患者の入院期間の見積りなど）

分類木(Classification Tree)

分類木は１つまたは複数の測定値から、あるデータがどのクラスに属しているのかを予測するために使用される。主にデータマイニングに利用されている技術である。データをパーティションに分割してから、各ブランチに更に分割するというプロセスを反復する。最終的にどのクラスに分類されたのかの判別は、終端ノードで行う。

○具体例

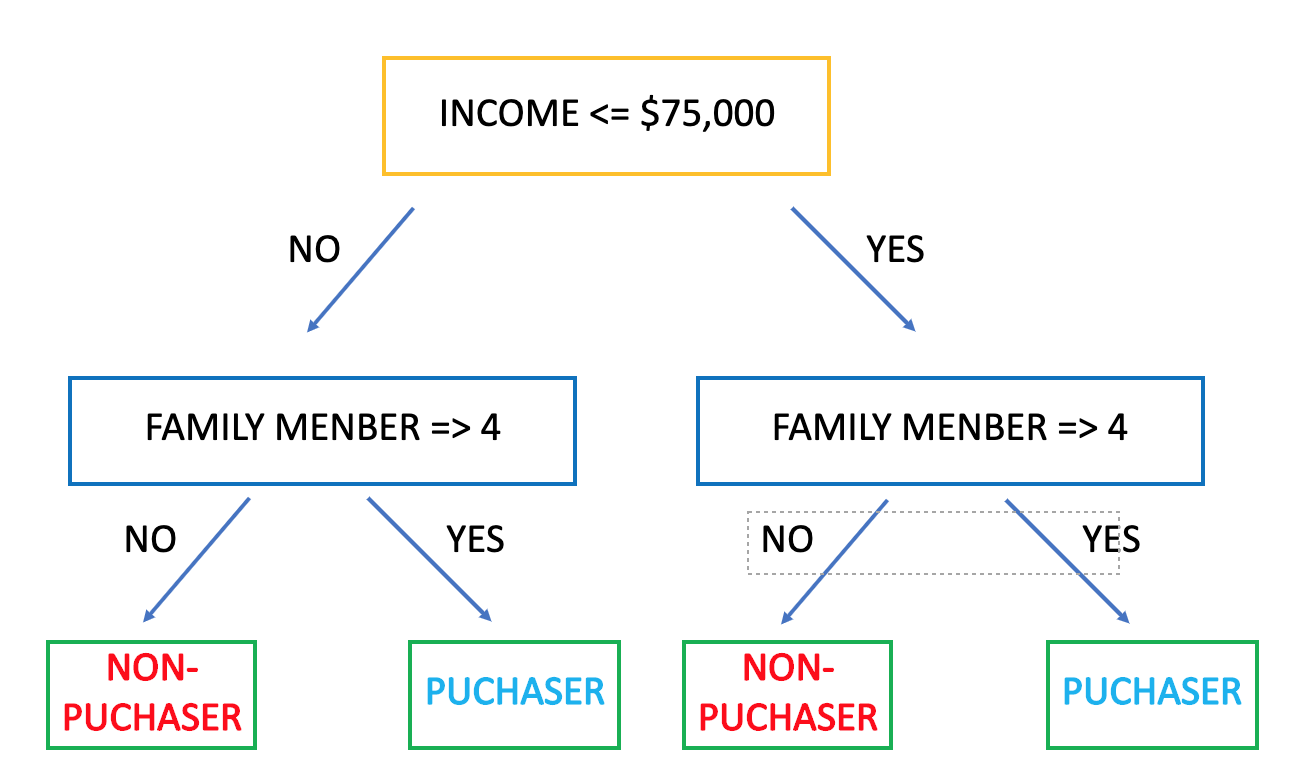
今回は購入者(Puchaser)と非購入者(Non-Puchaser)を分類する分類木を例に挙げる。先ず、各データについて分類ラベル（Puchaser/Non-Puchaser）が事前に分類されているデータセットを用意する。次に２つのノードに対してある条件式を元に各データを割り当てる。（図ではincome<=＄75,000かincome>$75,000で判定）その後、次のノードに割り当てる際にも別の条件を元に分割を適用していく。この分割の操作はこれ以上有用な分割ができなくなるまで行われる。（木の成長は以下の説明「木の剪定」、分割方法は「不順度」にて説明）

回帰木(Regression tree)

矩形内で一定の推定量をとる回帰関数である。 矩形は，(標準的な) ヒストグラム の場合とは異なり，その大きさが同じである必要はない。 回帰木は，ルールを2 分木として表現できるという独特の特徴がある。この特徴により，多くの説明変数がある場合にも推定値のグラフ表現を可能にする．

1.1 決定木の各種定義

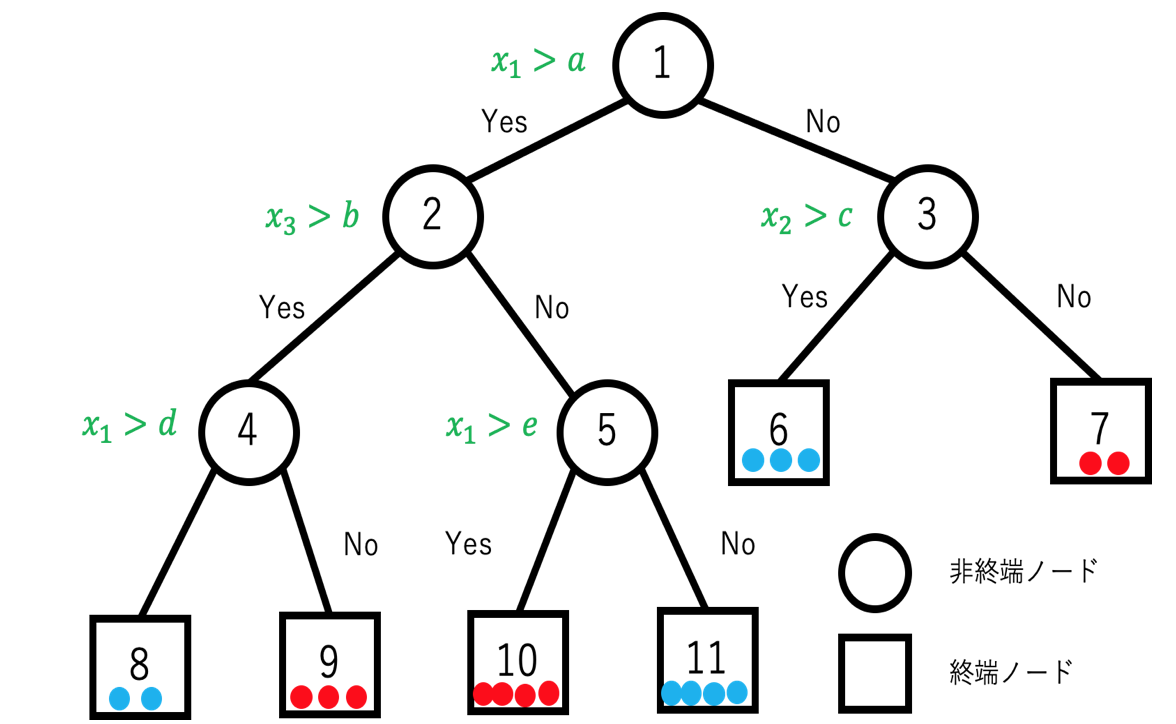
上図のノード全てに対して幅優先順(breadth first)で１からナンバリングして（これをノード番号とする）０でない整数の集合をTとする。またleft()、right()をそれぞれ２分岐したときの左側、右側のノード番号を与える関数とすると次の２つの性質を満たす。

1. 木Tに属する各ノードtについて、left(t)=right(t)=0（終端ノード）か、left(t)>t,right(t)>t（非終端ノード）のどちらかを満たす
2. 木Tに属する各ノードtについて、根ノードを除いてt=left(s)もしくはt=right(s)のどちらかを満たすsが一つ存在する。ここでsを親ノード、tを子ノードといい、s=parent(t)で表す。

ざっくりと説明すると木を構成するノードはどのクラスに割り当てるかを決める終端ノードとそれ以外の非終端ノードによって構成され、非終端ノードの分割先は多くても左側と右側に一つしか作成されず他のノードと合流することはないという意味である。

上記でも説明したようにノードのナンバリングは幅優先で行うため、right(t)=left(t)+1が成り立つ。またtからsへの一意のパスの長さをl(s,t)=mで定義する。

木Tの終端ノードの集合をとすると、差集合が非終端ノードの集合となる。

またTの部分集合をとし、以下の式との組み合わせが木となる場合に部分木となる。

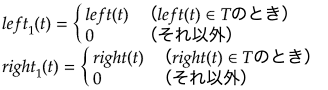
わかりやすいように上の図を使って説明をすると、={2,4,5}は上記式を満たすので、Tの部分木となる。一方で={2,4,5,3,6,7}は親がいないため、部分木とはならない。また、部分木の根ノードがTの根ノードと等しい場合はを剪定された部分木と呼ぶ。また任意のtとその子孫全てで構成される部分木を分枝と呼ぶ。

各終端ノードはそれぞれ一つの分割領域u(t)に属する。決定木では、各領域u(t)に特定のクラスを割り当てることで、入力データのクラス分類を行う。ここでクラスをとしたときに、終端ノードが表すクラスの事後確率を以下のように計算する。

クラスラベルのついた学習データ集合をとする。（木のノードと混ざりやすいが添字がついている方を学習データとする）クラスjに属する学習データ数をとすると、クラスjの事前確率は

となる。特徴空間はノードで分割ルールを経るごとに分割されていく。あるノードtに属する学習データの数をN(t)とし、j番目のクラスに属するデータをとする。必ず一つのクラスに属するので

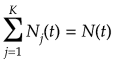
となる。j番目のクラスの学習データがノードtに属する確率が

であることからそれらすべての同時確率は

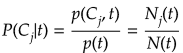
となる。上記式より周辺確率は、

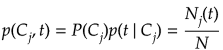
となるので、tにおけるj番目のクラスの事後確率は、

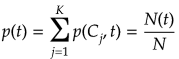
となる。よってノードtにおけるクラスの識別は上記式の事後確率が最大となるクラスを選択すれば良いので

となる。

1.2 ノードの分割ルール（不順度）

各ノードにおいて最も推定精度を向上させるための分割方法は、不順度と呼ばれる評価関数で評価することで選択する。学習データがN個であれば、N-1個の分割候補点がある。また、となり合った２点間の中間を候補点の一つとすれば、それはカテゴリー数だけ存在する。これらの中で選択される候補点は以下の式で計算される不順度に基づいて決定する。

○計算方法

ここであるノードtにおける不順度をI(t)とすると

ただし、

:クラスiに属するトレーニングサンプルの総数

N:トレーニングサンプルの総数

ここで、上記関数は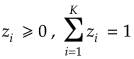に対して次の３つの性質を満たす。

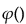• は、すべてのiに対して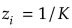のとき（どのクラスの事後確率も一様に等しい）最大になる。
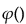• は、あるiについて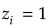のみを満たすとき、(ただ一つのクラスに定まる)最小になる。
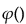• は、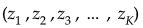に関して対象である。

代表的な不順度

①ノードtにおける誤り率(error rate)

②交差エントロピー、逸脱度(deviance)

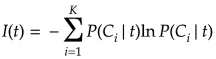
③ジニ係数(Gini index)

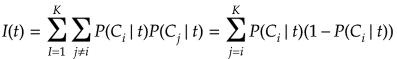
以上の①〜③のいづれかの方法を用いて不順度を計算し、不順度の減り方（勾配）が最も大きな分割を選択する。

特に③のジニ係数はCARTで用いられることが推奨されている（参考文献[4]より）。ノードtでi番目のクラスのデータが選ばれる確率とそれ以外のクラスに間違われる確率の積をすべて足し合わせる式となっているため、ノードtにおける誤り率となっている。この誤り率の減り方（勾配の計算で求める）が最大となる分割点を分割可能なすべての候補点の中から選択すれば良い。

1.3 木の剪定

剪定とは作成された木構造の一部分を削ることで木構造を簡易化して汎用性を保つ方法である。決定木は訓練データに基づいており、学習と分割が進みすぎると木が成長しすぎてしまい汎用性が低下してしまう。（学習データを判定する際に全く通用しなくなってしまう可能性が高くなる）そのため、決定木を作成する際には、推定精度が高く、かつ汎化性を保った木を作成するためには、ある程度の深さで木の成長を止めることが必要である。

○計算方法

木を構成した学習アルゴリズムに対して再代入誤り率を計算する。

終端ノードにおける誤り率は

M(t):終端ノードtにおける誤り数

N:総学習データ数

となる。（この誤り率は前節のジニ係数や逸脱度の値を用いても良い）

したがって木全体（終端ノードすべて）の再代入誤り率の推定値は、

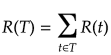
となる。

木構造の複雑さを終端ノードの数と再代入誤り率で評価する。

ある終端ノードにおける誤り率と複雑さのコストの和

:一つの終端ノードがあることによる複雑さのコスト(正規化パラメータ)

したがって木全体のコストは、

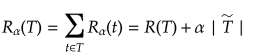
となる。この値が最小となるよう終端ノード数を調整する。しかしながら終端ノードが多くなるほど誤り率R(T)が高くなり逆に終端ノード数が減るほど誤り率が低くなる。そこでこの複雑さのコストが２つの要素の間のバランスを取る正規化パラメータ（調整パラメータでもある） の役割を果たしている。例えばこの値が小さくなると終端ノードを増やす方向に向かうため、大きな木が好まれる。

ノードtにおける再代入誤り率は、最大事後確率で決まるため、前節のノードtにおける誤り率と同じになる。つまり、

である。またノードtに学習データが属する確率をp(t)とすれば、

と書くことができる。

あるノードtを根ノードとする分枝（tのすべての子孫で構成される部分木のこと）をとする。もし、ならばtを終端ノードとしたときの木のコストより分枝を持っている方が小さいということになるので、分枝を残したほうが全体のコストは小さくなる。しかし、正規化パラメータの値を大きくするにつれて誤り率と複雑さのコストの値が等しくなり、その値は

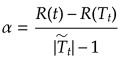
で与えられる。つまり、ノードtを残そうが剪定しようがコストは変わらないので、木が小さくなる方を優先するとして選定してしまって良いことになる。そこで、この正規化パラメータをtの関数とみなして

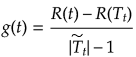
と定義する。木の剪定はすべてのノードに対してこの値を計算し、

とする。最小値をとるすべてのノードを終端ノードとし、その子孫を削除して木を剪定する。この操作を根ノードのみになるまで行う。

以上が剪定アルゴリズムであるが、再代入誤り率は剪定を進めるほど大きくなるため、どこで止めるべきかの情報が与えられていない。そのための基準を設ける必要があるがその方法としてホールドアウト法や交差確認法がある。しかしながらこれらは明確な基準値が設けられているわけではなく経験的にルールを設定することで基準作りを行っている。

2 応用

2.1 バギング(bagging)

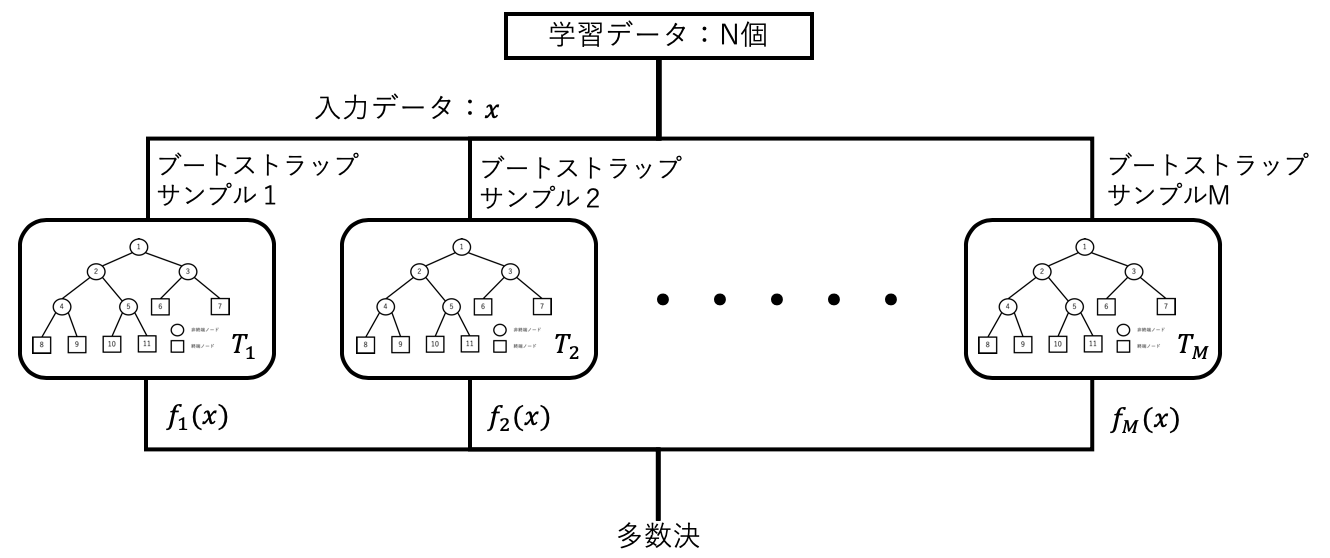
複数の決定木を組み合わせる方法の一つとしてバギングがある。Bootstrap AGGregatINGから派生しており、学習データのブートストラップサンプルを用いて複数の木で学習させ、それらの木で求めた結果に基づいて多数決で決定するという方法である。ブートストラップサンプルは学習データから重複を許したサンプリング(普通は学習データの数と同じだけ)を行い、新たな学習データを作製する、といった作業を木の数だけ繰り返す手法である。それぞれの木の判別性能はランダム識別より少し良ければ良いので弱識別器と呼ばれる。一つの決定木だけだと学習データに識別性能が大きく依存してしまうが、複数の結果の多数決を取ることでより安定で性能の良い判別器を構成することができる。一方でそれぞれの弱識別器はブートストラップサンプルに依存した性能であり、相関が高い性能になってしまうと、並列させるメリットが薄まってしまう。このような欠点を補うのが次節で説明するブースティングやランダムフォレストである。

2.2 ブースティング(boosting)

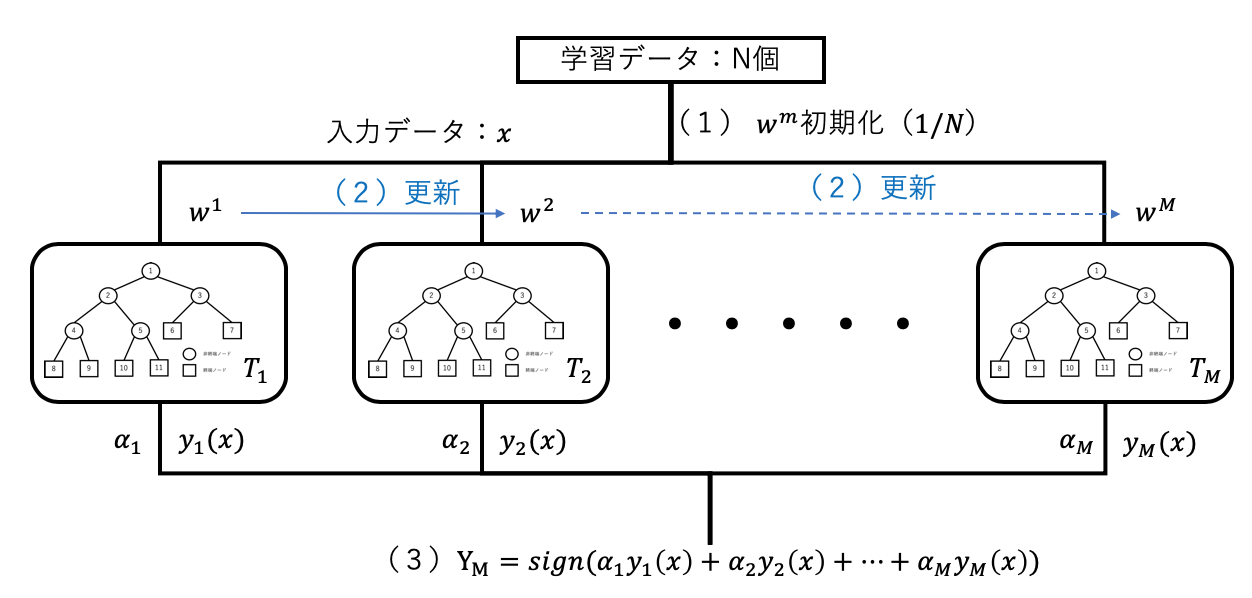
バギングは複数の弱識別器を並列に学習させていくが、ブースティングは直列的にし、前の弱識別器の学習結果を参考にしながら一つずつ弱識別器を学習する方法である。学習データは次の弱識別器にとって最も有益なものが選択される。代表的なブースティングアルゴリズムにアダブースト（adaptive boositng）がある。アダブーストは弱識別器の学習結果に従って学習データに重み付けが行われ、誤った学習データに対する重みを大きくして、正しく判別された学習データに対する重みを小さくすることで、後に学習識別器ほど、誤りの多い学習データに集中して学習するようにする方法である。

学習アルゴリズム

学習データ、教師データ、重み、弱識別器をそれぞれ,,,,とする。このときアダブーストのアルゴリズムは以下のようになる。

（１）重みをに初期化する。

（２）について以下を繰り返す

　　（a）識別器を重み付け誤差関数

　　　　　

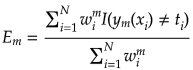
　　　　　が最小となるように学習する。は識別関数の出力が一致した場合0、一致しなかった場合1となる指示関数である。

　　（b）識別器に対する重みを計算する。

　　　　

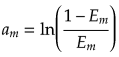
　　（c）重みを次のように更新する。

　　　　　

（３）入力xに対する識別結果を、

　　　

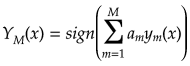
　　　に従って出力する。ただし、sign(a)は符号関数でありa>0なら+1、a=0なら0、a<0なら-1を出力する。（多数決）

（２）(a)は誤った学習データの正規化された重みの和である。これは誤差が小さいほど大きな値を取る。したがって誤りの小さなに大きな重みを与える。また重みの更新では、誤った学習データの重みがexp倍される。正しく判別されると重み付けはされないが、先程の（２）(a)の式で正規化されるため、相対的に小さくなっていく。また、弱識別器の数Mは多すぎると過学習が生じてしまうので、木の選定と同様に交差検証法などで選ぶ必要がある。

2.3 ランダムフォレスト(random forests)

バギングは前節で説明したように、決定木のような分散が大きな識別器に適した方法であるが、ブートストラップサンプリングによるため生成された決定木の相関が高くなってしまう。一般的に、分散を持つM個の独立な確率変数の平均

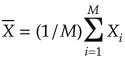
の分散は

であるが、２つの間に正の相関がある確率変数の場合には、平均の分散は、

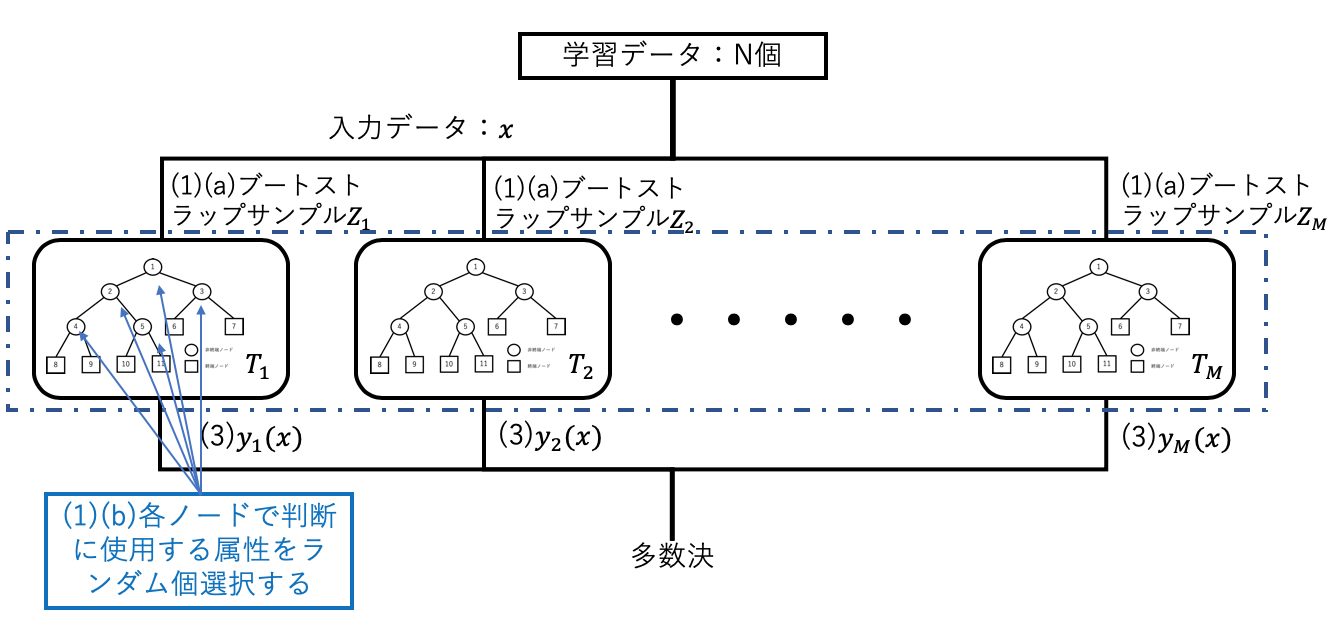
サンプル数Mを多くすれば上記式の第一項は無視できるが第2項は変化しない。ランダムフォレストはこの第2項のを減少させる仕組みを取り入れたバギング手法の一種である。決定木の各非終端ノードにて判別に用いる特徴をランダムの個数選択することで、相関の低い多様な決定木が生成されるようになっている。

学習アルゴリズム

（１）について以下を繰り返す

　　　（a）N個のd次元学習データ（入力データx）からブートストラップサンプルを生成する。

　　　（b）を学習データとして、以下(ⅰ) 〜(ⅲ)の手順によって各非終端ノードtを分割して決定木を成長させる。

　　　　　　(ⅰ)d個の特徴からランダム個数d'を選択する。（一般的には平方根を四捨五入した個数が望ましいが問題によって最適は異なるので都度調整したほうが良い）

　　　　　　(ⅱ)d'個の中から、最適な分割を与える特徴（ランダム）と分割点を求める（不順度より判断）。

　　　　　　(ⅲ)ノードtを分割点でleft(t)、right(t)に分割する。

（２）ランダムフォレストを出力する。

（３）入力データに対する識別結果を出力する。２クラス分類なら01で判断し、多数決でランダムフォレストの識別結果を選択する。

SVMやアダブーストが２クラス分類の識別器であるのに対して、ランダムフォレストは多数決によって多クラスの分類に容易に拡張が可能である。一方でデメリットとして各決定木で学習を進める際に、データが少ないと過学習になりやすくなってしまうという点がある。

3 シミュレーション

決定木アルゴリズムCARTを用いた性能評価をAzure MLで行う。評価は以下の2点である。

• 森のサイズと推定精度

各アルゴリズムで使用する決定木の数を調整し、推定精度にどのような影響が生じるのか評価した。それぞれで作成したモデルは次節で説明する。

• 学習曲線

学習データの数を調整し、推定精度にどのような影響が生じるのか評価

3.1 シミュレーション１（森のサイズと推定精度）

ブースティング、ランダムフォレストを用いると、森のサイズ（決定木の数）による推定精度の変化を評価することができる。一般的に森のサイズが大きいほど分散が小さくなるので推定精度は良くなることが予想される。以下でモデルの作成に関する説明を述べる。

モデルの作成

下図のフレームワークを用いてそれぞれのシミュレーションを行う。各フェーズについて説明する。

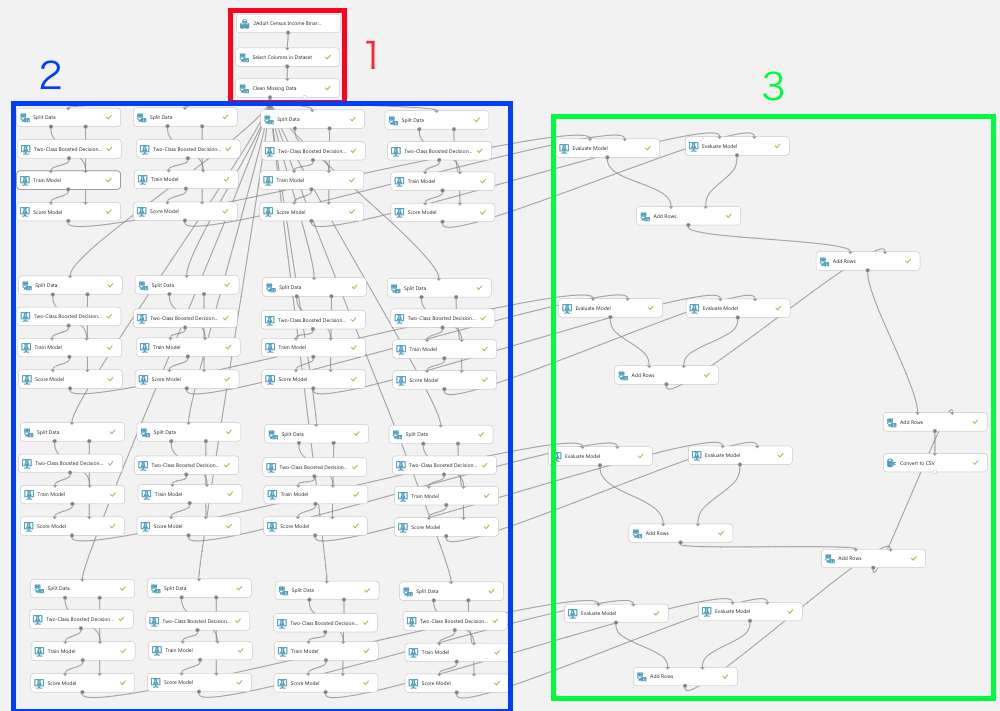
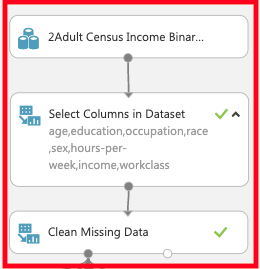
フェーズ1 データセットの整形

データセットはAzure MLに標準で用意されている「2Adult Census Income Binary Classification dataset.csv」を使用している。属性として年齢、学歴、収入などの特徴軸があり判定対象は「性別」とし、サンプル数を10000用意している。

「Select Columns in Dataset」ではage,education,occupation,race,sex,hours-per-week,income,workclassをcolumnとして選択し、「Clean Missing Data」で"Null"のサンプルを取り除き以下の図のようにつなぐ。

フェーズ2 データの学習とテスト

フェーズ２では各アルゴリズムの学習とテストを行うモジュールで構成される。はじめに「split data」でデータセットを学習データ100個とテストデータ9900個に分割する。次にブースティング「Two-Class Boosted Decision Tree」及びランダムフォレスト「Two-Class Decision Forest」と「train model」を用いて「性別」の判定に関する学習を行う。ここで、それぞれのモジュールにて木のサイズを1〜100まで（計16種類）を設定する。学習させたモデルに対して「split data」からテストデータを「score model」に読み込ませ、以下の図のようにそれぞれつなぐ。

○ブースティング

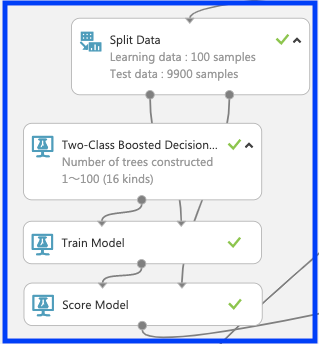
○ランダムフォレスト

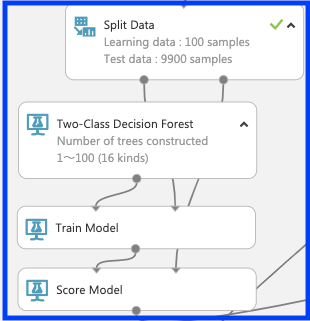
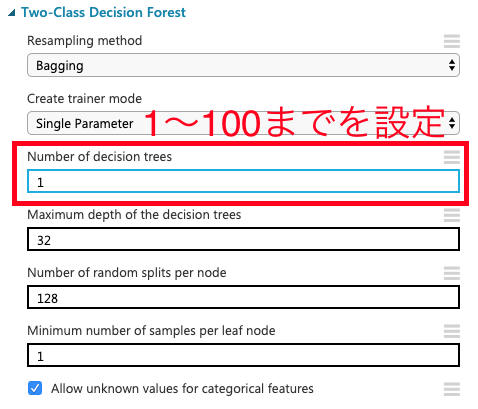
フェーズ3 評価と結果の統合、csvファイルへの出力

フェーズ２で行った学習とテストに基づいて「evaluation model」で予測精度の評価を行う。評価を行った後はそれぞれの森のサイズで行った値を集計するため「add rows」でデータの統合を行う。

すべてのデータの統合が完了したら、エクセルにてグラフの作成を行うため、「convert to csv」によりcsvファイルへのエンコーディングを行う。

シミュレーション結果

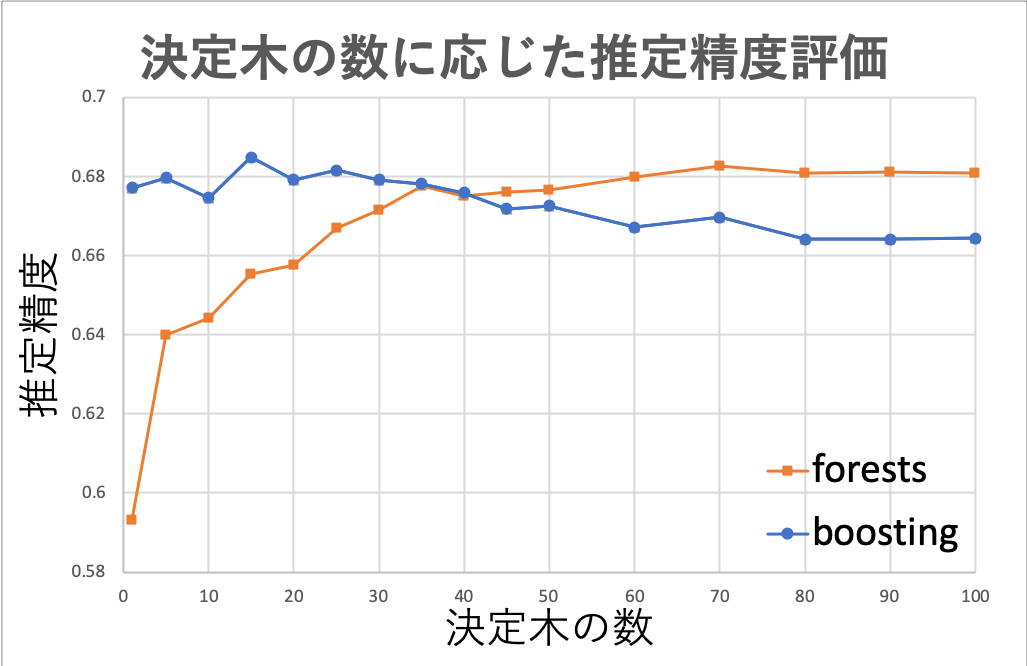
シミュレーション結果は上記のようになった。学習したデータセットによってそれぞれのアルゴリズムの予測精度は大きく変化するが、今回の結果としては森のサイズが小さいときにはブースティング、森のサイズが大きくなるほどランダムフォレストの予測精度が高いことがわかる。特にブースティングは森のサイズが大きくなることによる予測精度の向上が見受けられなかった。これは誤りやすいデータと誤りにくいデータの相関が大きくアルゴリズムの特性を活かすことができなかった点が考えられる。一方でランダムフォレストは森のサイズが大きくなるほど予測精度は良くなっているが、68％付近にて飽和している。これ以上の予測精度の向上には属性を増やすことが挙げられる。

3.2 シミュレーション２（学習曲線）

決定木に限らず、学習量によってどの程度正確な学習モデルが作成されるかが変わってくる。極端に学習データが少ないと分散が非常に大きく、一つのデータに対する依存度が高くなってしまうことが予想できる。ここでは学習量が各アルゴリズムにて推定精度にどのような影響を及ぼすか評価を行う。

フェーズ1 データセットの整形

前節と同様のため割愛

フェーズ2 データの学習とテスト

各アルゴリズムでの設定を以下の図のように行う。

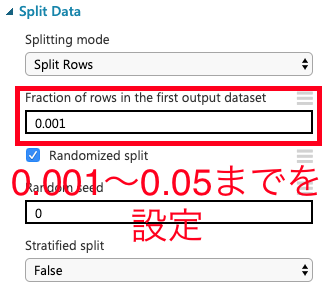
「split data」

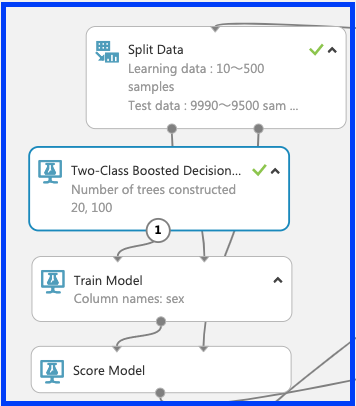
○ブースティング

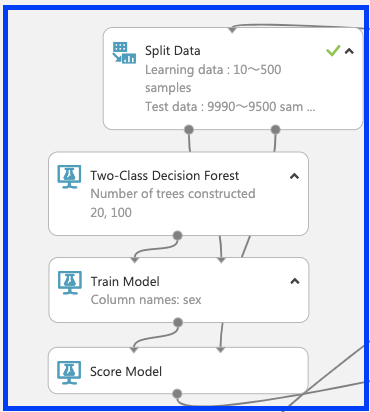
○ランダムフォレスト

フェーズ3 評価と結果の統合、csvファイルへの出力

前節と同様のため割愛

シミュレーション結果

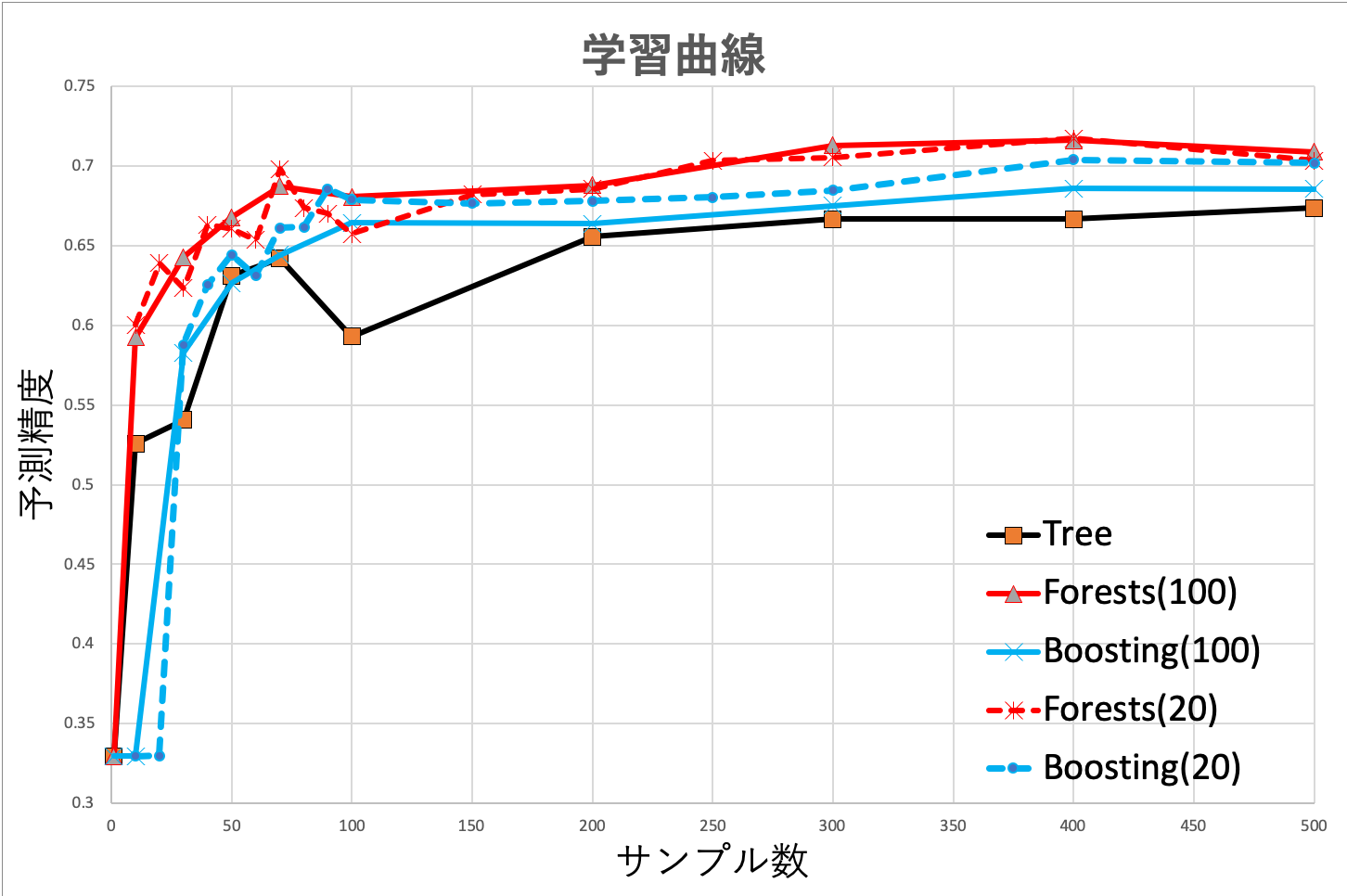
シミュレーション結果は上記のようになった。ランダムフォレスト（森のサイズ100）が最も精度がよくなっていることがわかる。また、全体的に学習量が増えるほど推定精度がよくなっており、それぞれのアルゴリズムごとにある値で飽和している。また、森のサイズが小さいもしくは決定木1つのみの場合は分散が大きいため、推定精度の安定性が低い。前節でも説明したようにブースティングに関しては森のサイズが大きくなることによって推定精度の劣化が見受けられる。

終わりに

この記事では非線形分類や回帰を行うことができる決定木全般に関する理論とシミュレーションを行った。今は過ぎしマイニングブームでもC4.5やCARTなどは推定精度が高いことから頻繁に活用されていたアルゴリズムである。個人的にはNNやSVMよりも理解しやすいため、是非ロジスティック回帰と併せて学習することをおすすめしたい。

その他、Microsoft Azure Machine Learningでやってみた記事も参考にしてください！

・ロジスティクス回帰も用いたIris Two Class Dateの分類

・分位点回帰を用いた飛行機遅延予測

・パラメーターチューニングを行う

・ランダムフォレスト回帰を用いた人気ブログタイトル予測

参考文献

○決定木について

[1]https://ja.wikipedia.org/wiki/%E6%B1%BA%E5%AE%9A%E6%9C%A8　

[2]https://dev.classmethod.jp/machine-learning/2017ad_20171211_dt-2/　

[3]https://qiita.com/3000manJPY/items/ef7495960f472ec14377

[4]https://www.researchgate.net/publication/265031802_Chapter_10_CART_Classification_and_Regression_Trees

○分類木について

[5]https://www.solver.com/classification-tree　

○回帰木について

[6]https://www.solver.com/regression-trees　

○不順度について

[7]http://darden.hatenablog.com/entry/2016/12/09/221630　

○ランダムフォレストについて

[8]https://link.springer.com/article/10.1023/A:1010933404324　

○ブースティングについて

[9]https://www.frontiersin.org/articles/10.3389/fnbot.2013.00021/full