はじめに

　今回はロジスティック回帰についてやっていこうと思います。まずはロジスティック回帰の概要を説明して、最後には実際にAzureでiris(アヤメ)のデータでロジスティック回帰を使っていこうと思います。

勾配降下法

　ロジスティック回帰でパラメータの値を決めるときに勾配降下法を用いるので、簡単に説明をしておきます。

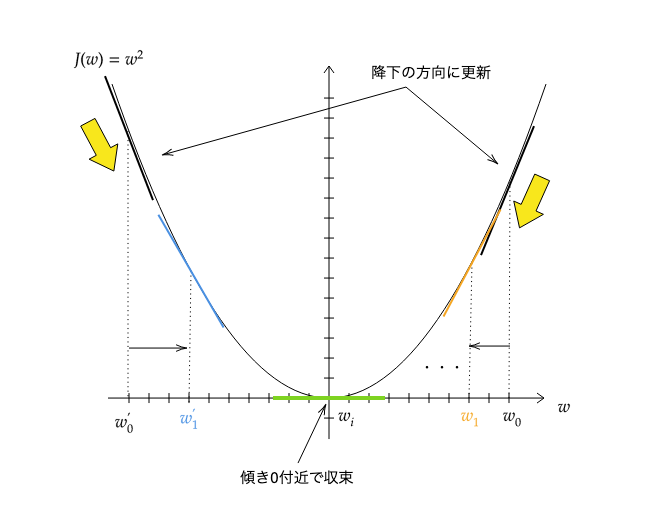
　勾配降下法は、ある関数J(w)が最小となるwを求める際に、あるwでの傾き(勾配)を求めて、降下の方向(傾きが小さくなる方)にwを更新し、その更新をwが収束する(勾配≒0)まで繰り返して収束したところでのwでJ(w)が最小であると決めます。その更新の式は次のようになります。

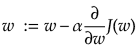
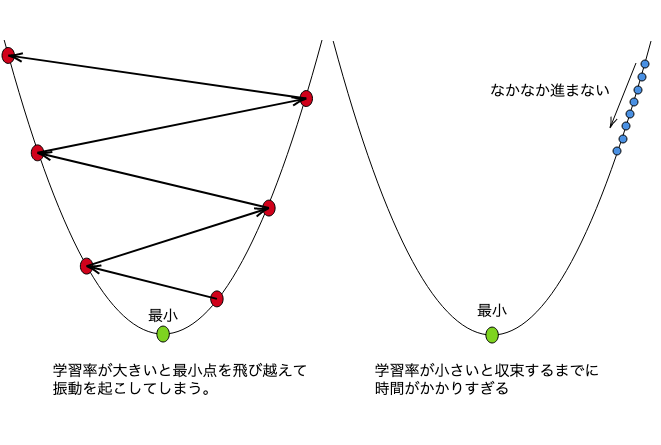
ここでのαは学習率といい、降下の方向にどのくらいwを移動させるかを表します。ここでαが大きすぎると最小となる点を更新の際に飛び越えて振動してしまいます。逆に小さすぎるといつまでも収束しないので、適当な値をαに決めなければいけません。またwがn次元ベクトルの場合は、そのn個について同時に更新するということにも注意が必要です(詳しくはロジスティック回帰の説明中)。

ロジスティック回帰とは

　ロジスティック回帰とは、ある事象が発生するかどうかを、その確率を出すことにより判定することに使われる手法で、目的変数が2値のときに使われるアルゴリズムです。具体的に言うと、アヤメの花の種類A,B(目的変数)があったとき、その花の花弁の大きさなど(説明変数)から種類を判定したいときにロジスティック回帰を使うことで判定することができます。それではロジスティック回帰の流れを見ていきましょう。

　線形回帰では目的変数yを、パラメータwによって決められる説明変数xの関数h(x)で予測しました。

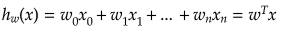
　ロジスティック回帰では、このh(x)を下図のシグモイド関数に入れた形にして、その値を0以上1以下にすることで2値(目的変数y=0,1)の分類を可能にします。

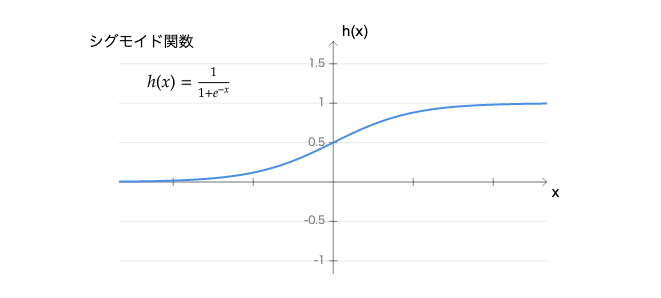
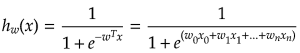
このh(x)はy=1である確率として解釈できるので、

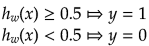
のように分類する規則を決めて判定することができます。

　では、パラメータwを決め方について見ていきましょう。結論から言うと次のような目的関数J(w)を最小にするようなwを決めます。

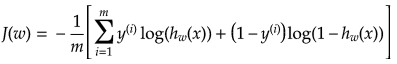
目的関数はy=0,1を正しく判定したときに最小(→0)、全然一致しないとき最大(→∞)になるように設定します。そこで、h(x)≧0.5(より1に近い)のときy=1と予測し、h(x)<0.5(より0に近い)のときにy=0と予測することから、logの性質を利用して目的関数を決めました。考え方は次のようになります。

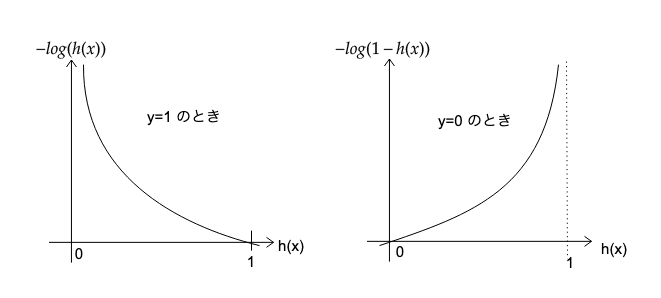
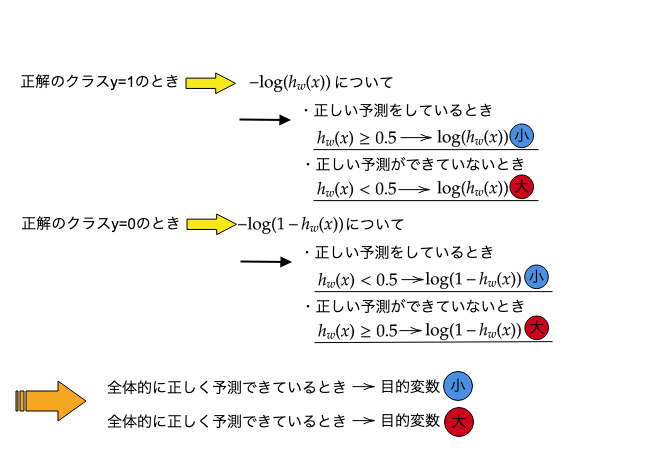
これで目的関数の設定はできたので、これが最小となるパラメータwを決めていきましょう。ここで使われるのは勾配降下法です。

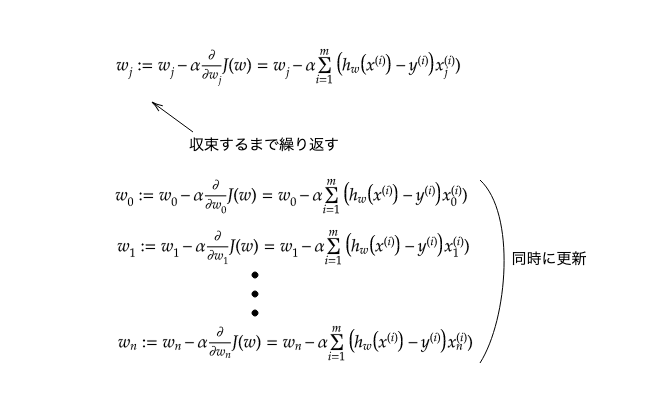
ここでの勾配降下法は上の式において、j=0,1,...,nそれぞれについて同時に更新して、wの値が収束するまで更新を続けてwを決定します。

目的関数を最小とするパラメータwを決めることができたので、ロジスティック回帰による予測モデルが完成しました。これで未知のデータに対して予測することができます。

これで流れは掴めたと思いまので、実際にAzureを使ってロジスティック回帰を実行してみましょう。

Azureでロジスティック回帰

　今回はAzureのサンプルデータのIris Two Class Dataを使います。はじめにデータを見てみると(画像はデータの一部)、目的変数に2種類のiris(アヤメ)のクラスを0,1で与え、説明変数にsepal-length(がく片の縦幅)、sepal-width( がく片の横幅)、petal-length(花びらの縦幅)、petal-width(花びらの横幅)の4つを与えています。

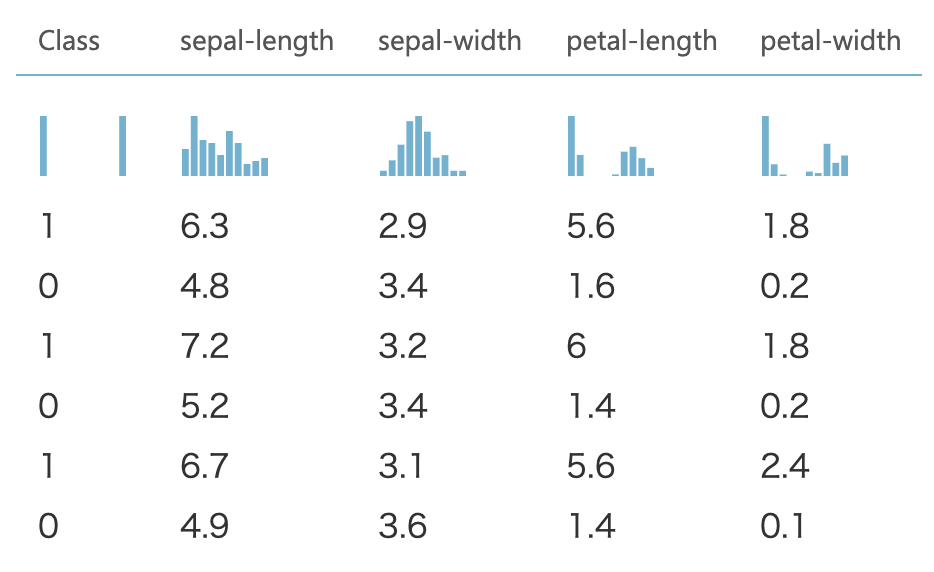
このデータに対してロジスティック回帰を行います。

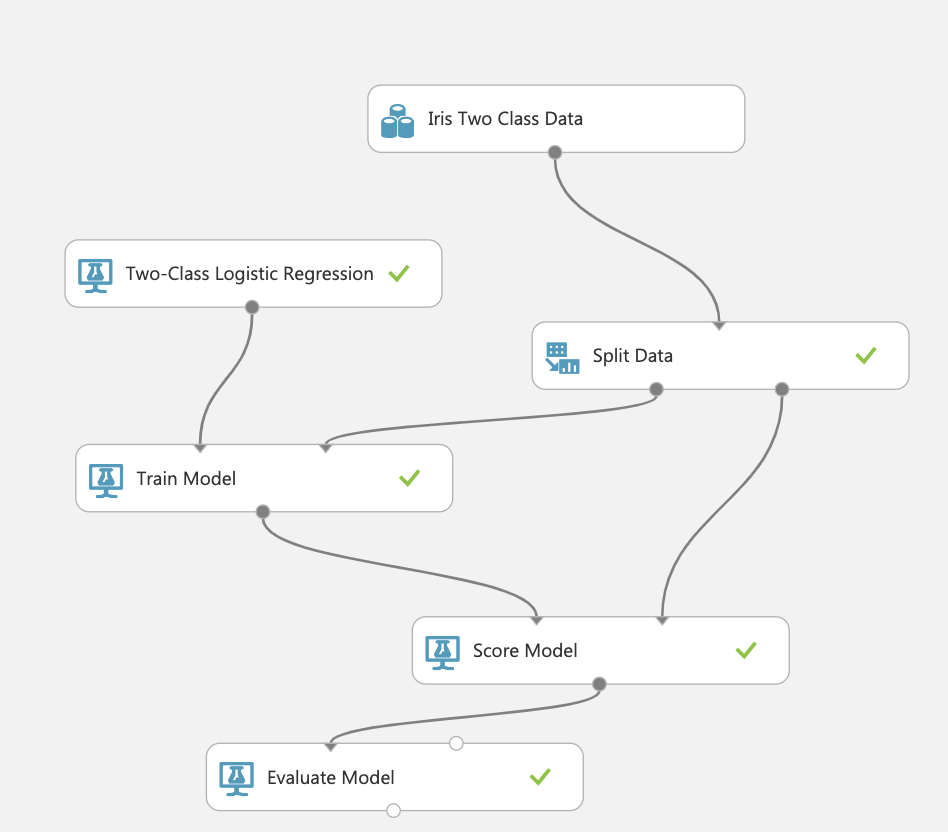
Azureでは上のようにするとロジスティック回帰ができますが、流れを整理すると次のようになります。

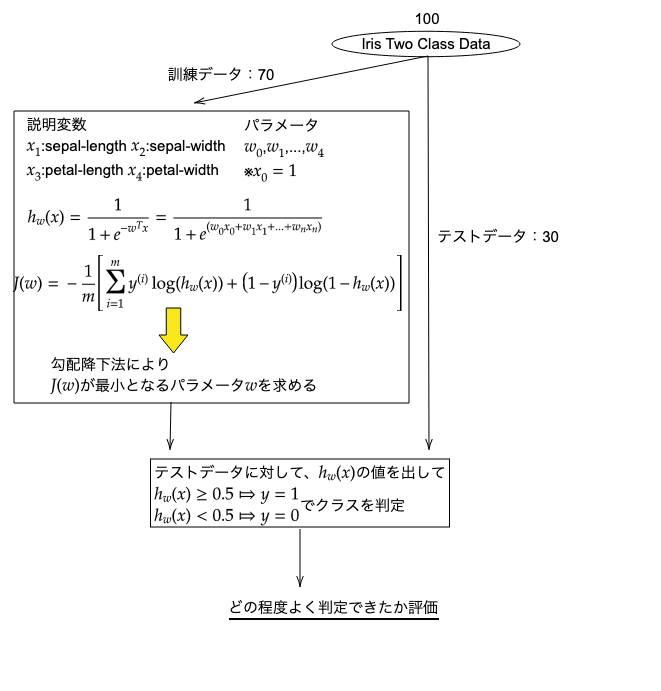
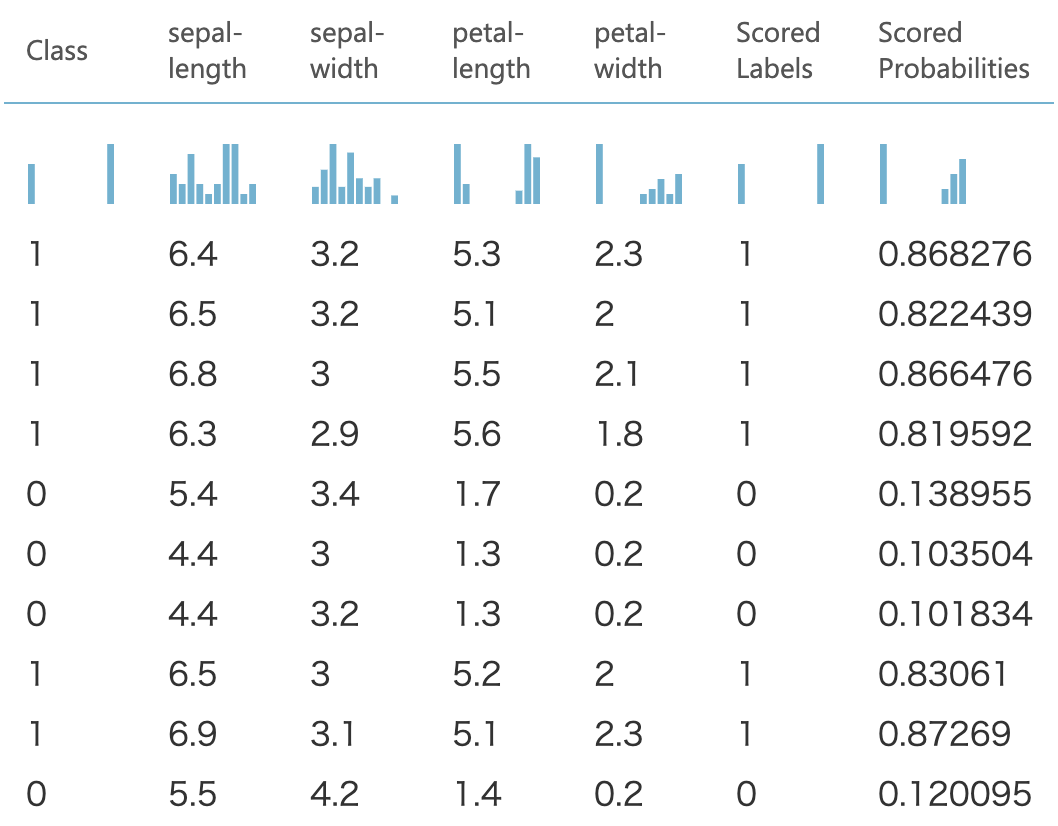
結果を見ると、一番右の列のScored Probabilitiesはクラス1である確率(h(x))を表していて、0.5以上でクラス1とScored Labelsで判定しています。ROC曲線で評価してみると、

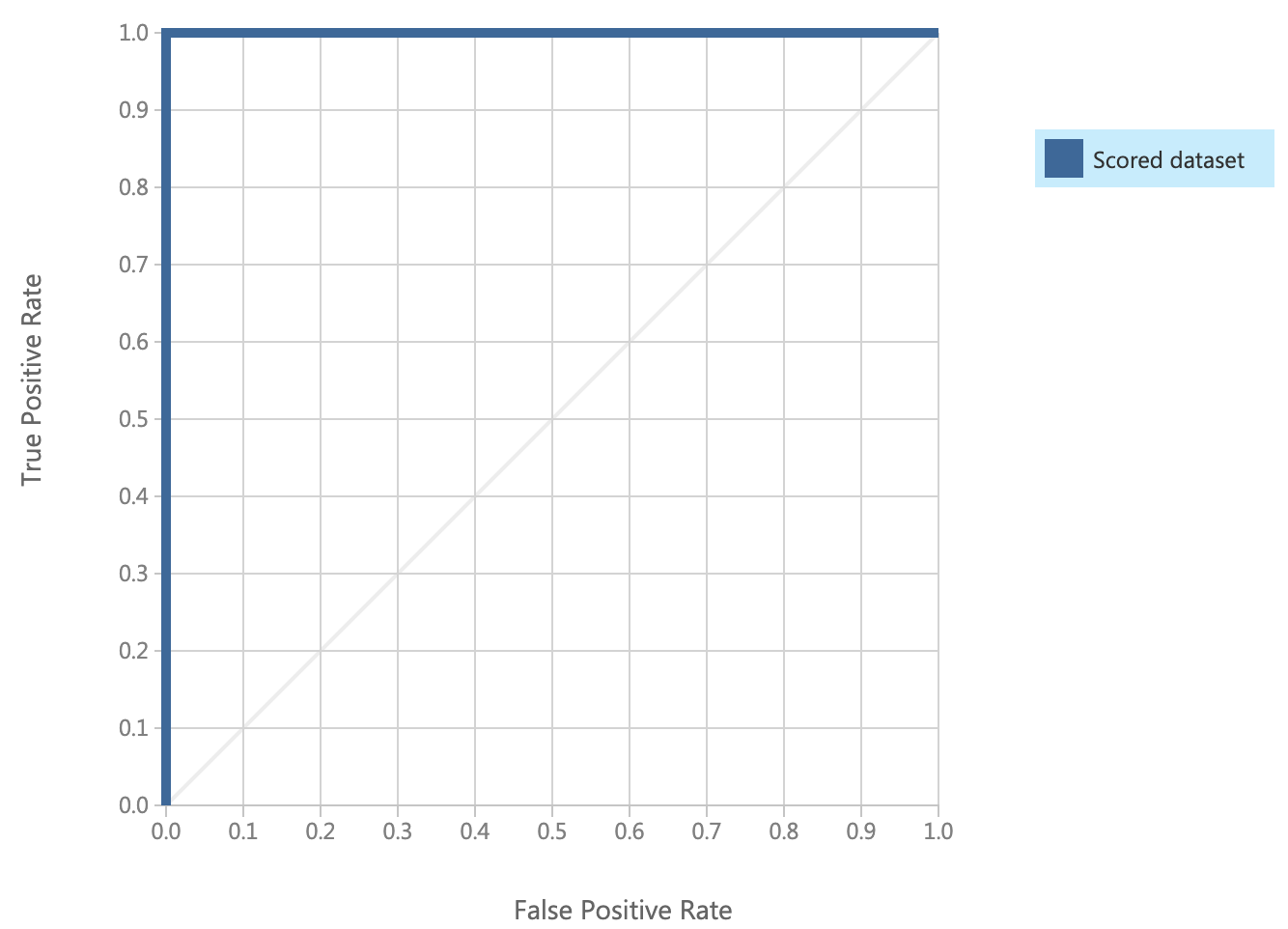
完全に予測することができています。今回はサンプルデータなのでこんなにうまく予測できていますが本来はこんなにうまくいきません。

次に縦軸にそれぞれの説明変数ごとにとり、横軸にScored Probabilitiesを取った散布図を見て、どの説明変数が判定に影響を与えているかを視覚的に考えてみます。

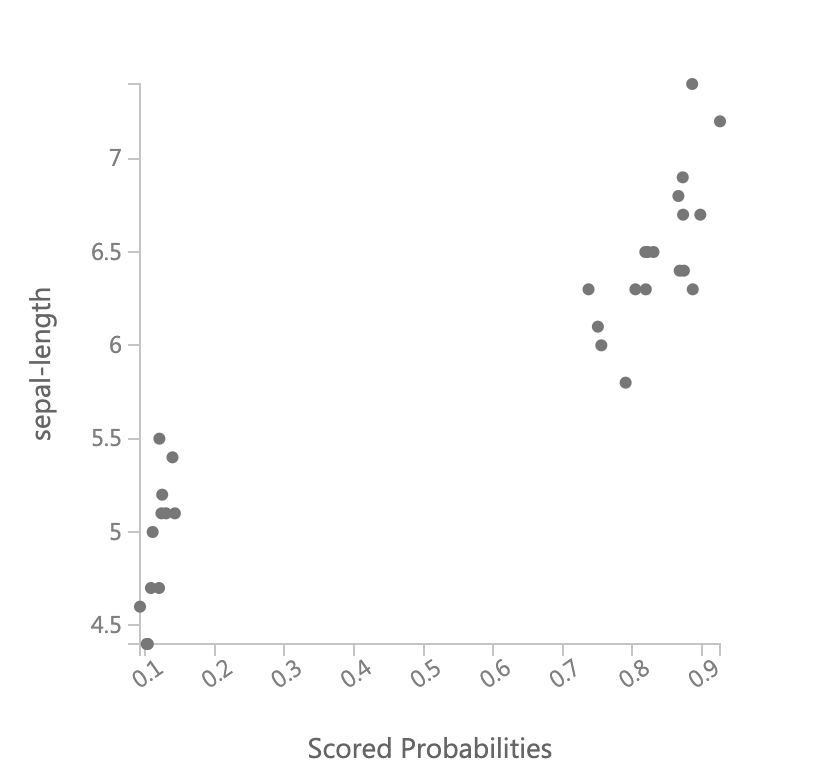
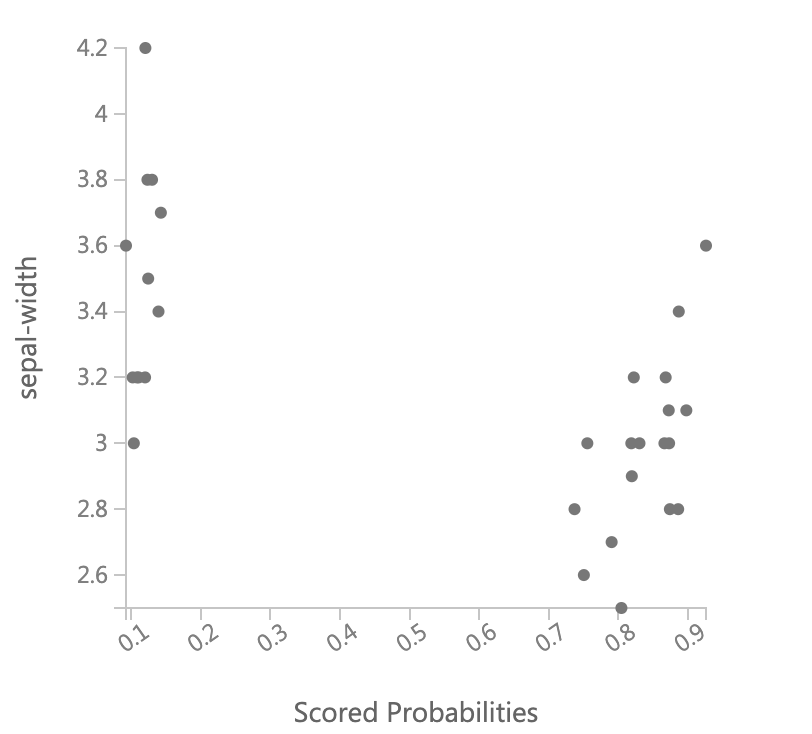
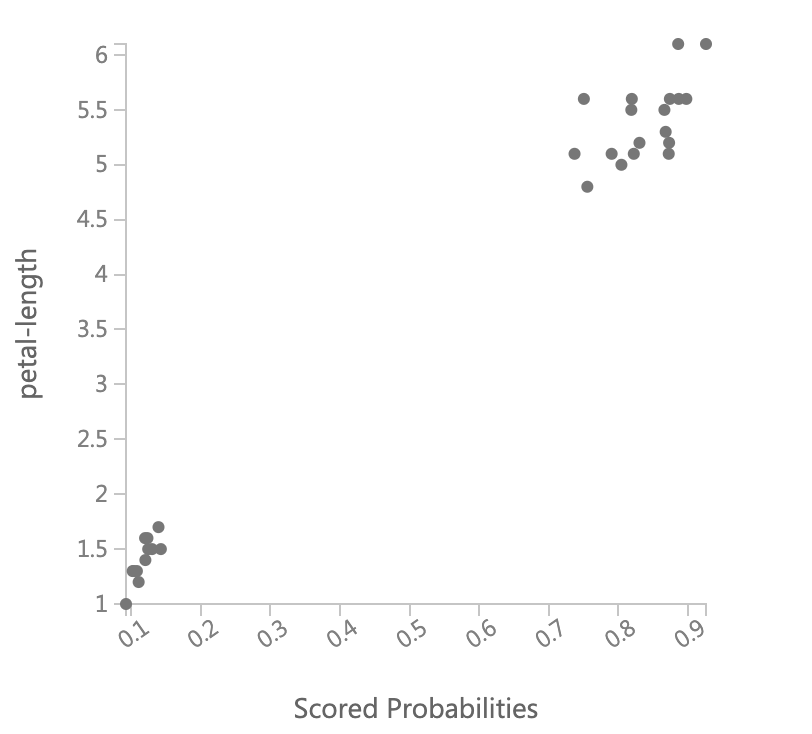
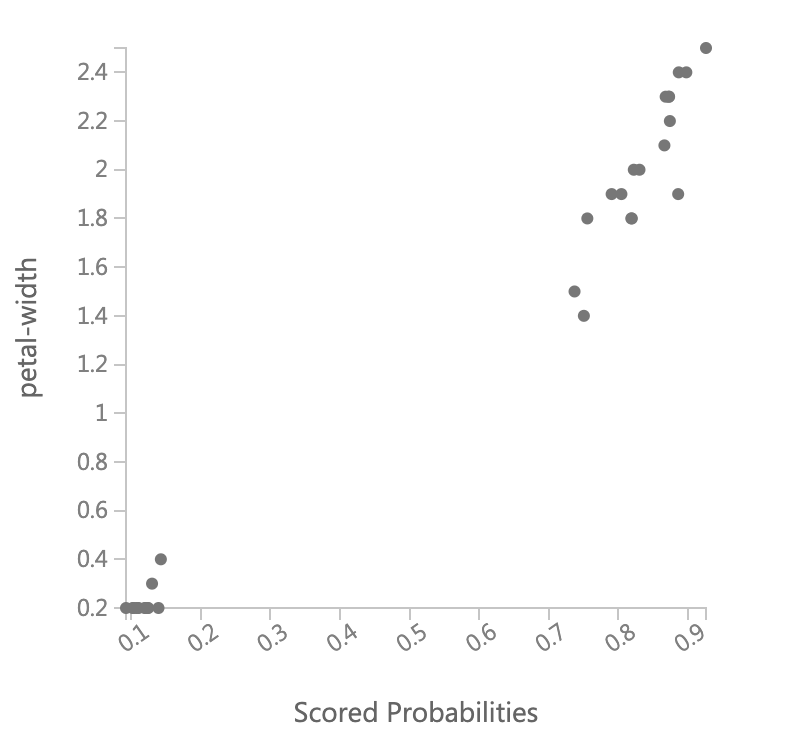
これを見ると、petal-lengthとpetal-widthは明確にその値が大きければクラス1に属する確率が高く、小さければクラス1に属する確率が低いことがわかります。sepal-lengthもpetalよりは弱くなりますが同様の傾向があることがわかります。それに対してsepal-widthは同じくらいの値を取っていても、クラス1である確率が大きかったり小さかったりと明確には言えません。更にどちらかと言うと、値が小さい方がクラス1の確率が高くなっています。その関係がパラメータに現れていることを確認すると、

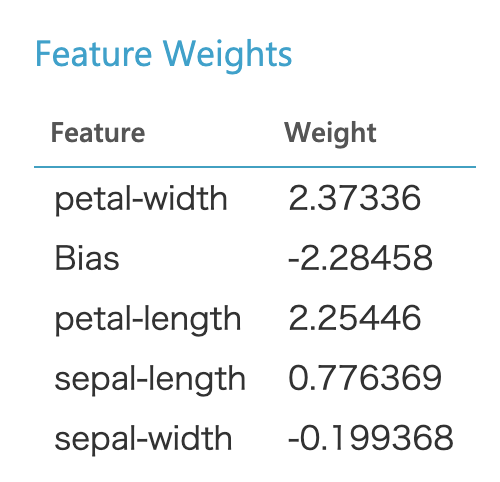
petal-length、petal-widthのweight(係数、重み)が大きくなっていて、sepal-lengthのweightがそれに比べ小さく、sepal-widthのweightは負でかつその絶対値は小さくなっていますので、散布図の傾向はしっかりとあたっています。今回はサンプルデータでやったので、かなりうまくいってわかりやすかったですが、本来はここまできれいにはならないでしょう。

まとめ

　今回はロジスティック回帰についてやりました。非常に有名で基本的な手法ですのでしっかりと理解しておくと良いでしょう。

その他のMicrosoft Azure Machine Learning Studioでやってみた記事も参考にしてください！
決定木アルゴリズムCARTを用いた性能評価
分位点回帰を用いた飛行機遅延予測
パラメーターチューニングを行う
ランダムフォレスト回帰を用いた人気ブログタイトル予測

参考文献

Coursera 機械学習 Andrew Ng