このブログはそもそもパラメータという言葉をよく耳にするが、どのように決定しているのか知りたい人(機械学習の初歩的な数学の理論を知りたい人)向けです。少し数学的な計算も入ってきます。

学習とは、仮定から導き出した誤差関数を最小に，あるいは尤度関数や事後分布を最大にするパラメータを求めることでした。そのうち今回は尤度関数と勾配法について説明していきたいと思います。

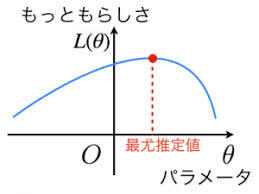
パラメータとはどういう設定値や制限値で機械学習の予測モデルを作るのかを示すものです。イメージとして、あとで定義する尤度関数が下のグラフのようになっている時、尤度関数の最大値を取るθを求めるという作業です。

目次

1. 最尤推定法

2. 勾配法

3. 最尤推定法と勾配法の問題点

1.最尤推定法

確率分布は既知ですが、ある母数(パラメータθ)が未知な母集団を考えます。

この場合、この確率分布が連続型であるならば、確率分布はθに依存する関数と考えられ、f(x,θ)と表します。

この母集団から独立にn個標本を抽出した時のデータがx1,x2,....,xnの値をとる確率は、L(θ)=f(x1,θ)f(x2,θ)....*f(xn,θ)と考えられ、L(θ)を尤度関数といいます。

まず具体例を見てみましょう。

正規分布の平均、分散の最尤推定

X~N(μ,σ^2)とします。(N(μ,σ^2)は平均μ、分散σ^2の正規分布)

すると以下のように平均と分散の最尤推定値が求められます。
正規分布の確率密度関数を以下のように与えられます。

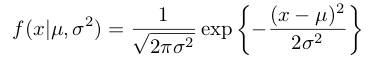
(x1,.....,xn)というデータが与えられたとすると、尤度関数は次のようになります。

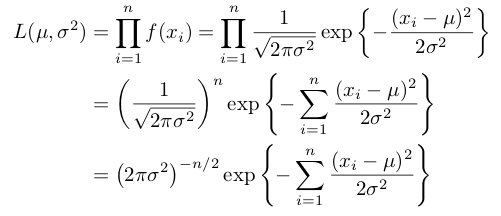
なので両辺に自然対数を取ると、以下のように対数尤度関数が導かれます。

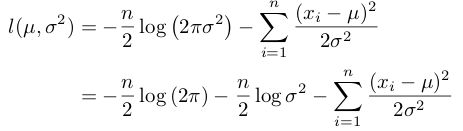
これから平均μを最尤推定法により推定します。対数尤度関数をμに関する関数と見て偏微分し、その結果が0となる値を求めます。

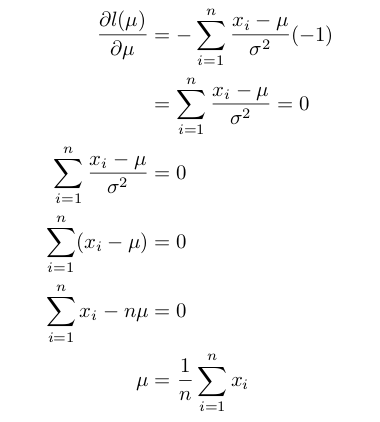
次に、分散σ^2を最尤推定法により推定します。対数尤度関数をσ^2に関する関数と見て偏微分し、その結果が0となる値を求めます。

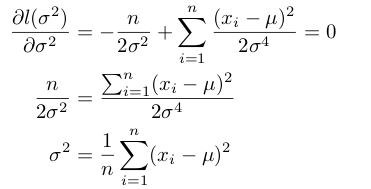
以上が最尤雨推定法の概要です。

2.勾配法

勾配法は最小値や最大値を求めるためのアルゴリズムで、解析的に解くことが困難な問題に用いられます。

「解析的に解けない」とは、ある関数に対してうまく微分ができない状態や実際に数値として表すには禁じせざるを得ない状況のことです。

勾配法は解析的に解くのが困難な時に有効なアルゴリズムで、最適化問題などに用いられます。 具体的な方法を解説していきます。

1. 適当に初期点を決める

2. 今いる位置における関数の値が最も小さくなる方向を計算する

3. その方向に微小単位で移動する

その後は、2,3の手順をひたすら繰り返し、収束した場合、この繰り返しを終了します。

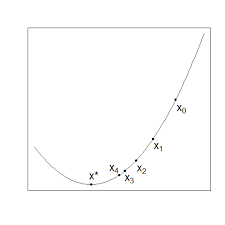
この例は解析的にも解けますが、勾配法を使って説明するとまずはじめにx0という点を初期値として選択します。

次に、今いる位置における関数が小さくなる方向を計算します。これは図からわかる通り、x1の方向に近づく方向になります。

ここからは今までの操作の繰り返しです。

すると、図からX*という点で今まで同様左側に移動すると関数の値が大きくなってしまいます。

つまり、図の範囲でパラメータとして最も良いものはx*ということになります。

3.最尤推定法の問題点

データ数が少ない時に偏りがあることです。

この例としてコインの裏表を3回投げるという試行を考えます。 もし、表が三回連続で出てしまった時、表の出る確率は最尤推定法で求めると1となりますが、本来表の出る確率は1/2であるはずです。 これがデータ数が少ないことによるパラメータの偏りです。

サンプルから構造を推測する モデルにおいては適していません。

例えば、混合正規分布、混合２項分布、神経回路網、ベイズネットワーク、 隠れマルコフモデルなどのもウール構造を持つモデルについては最尤推定法は適していません。 つまり、「尤度関数が最尤推定量の近傍でだけ 大きな値になる」という条件が最尤推定が安全に使えるための条件です。

また、尤度関数は常に解析的に解けるものではないので、最尤推定以外の方法でパラメータを求める必要があります。(勾配法など) 必ずしも全ての試行が確率分布に従うとは限らず、確率密度のある点における接線の傾きを測る勾配符が用いられるケースがあります。