線形モデル(linear model)は、実用的に広く用いられており、入力特徴量の線形関数(linear function)を用いて予測を行うものです。
まず、説明に入る前に言葉の定義から紹介します。

線形回帰

データがn個あるとした時にデータの傾向をうまく表現することができるy=w_0×x_0+....+w_n×x_n というモデルを探し出すこと

正則化

過学習を防いで汎化性を高めるための技術で、モデルに正則化項というものを加え、モデルの形が複雑になりすぎないように調整している
　(モデルの係数の絶対値または二乗値が大きくなってしまうと、訓練データのモデルに適合しすぎて、テストデータのモデルの当てはまりが悪くなる過学習という現象が起こるので、過学習を避けるために正則化項をつけている)

重み

説明変数（求めたいものに作用する変数）が目的変数に与える影響度合いを表現したものです。例えば上の線形回帰モデルでいえばw1やw2など説明変数の係数が重みに当たる

コスト関数

構築したモデルがどれだけ悪いかを測定する関数
機械学習の分野ではコスト関数を最小化することがモデル構築では重要となる

モデルの比較

Ridge回帰とLasso回帰は大きな差があるわけではありません。
根本の考えは同じだが、視点を変えてみたようなものです。
まずは根本の考えについて(E:誤差関数 , λ:正則化パラメータ)
S=E+λ(Lpノルム)　について考えます。

p=1の時がRidge回帰、p=2の時Lasso回帰である

ノルムの定義は以下の通りです。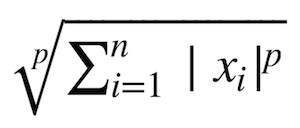

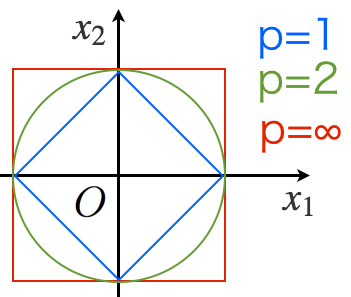
モデルの特徴をノルムの次元数から推測すると以下のことがわかります。

1.L1ノルムはパラメータの一部を完全に0にするため、モデルの推定と変数選択を同時に行うことができる
2.次元数>>データ数の状況で強力
3.L2ノルムは微分可能であり解析的に解けるが、L1ノルムは 解析的に計算出来ない
4.L1ノルムには様々な推定アルゴリズムが提案されている

以上のことから、常にどのノルムが一番優れているということはほとんどありません。

L1ノルムはパラメータが0になりやすく、正則化の影響が非常に強いことに対してL2ノルムは過学習になりやすく、正則化の影響が少し弱いです。
Ridge回帰は他と余りにもかけ離れたデータの重みを0にする事で、学習用データから削除するもの
Lasso回帰は他と余りにもかけ離れたデータの大きさに応じて0に近づけて、学習結果を滑らかにするもの
ということが分かりました。
つまりRidge回帰は訓練データに対する精度は高いですが、テストデータに対する精度は少し低くなります。
一方、Lasso回帰は訓練データに対する精度はRidge回帰に比べ低くなりますが、テストデータに対する精度はRidge回帰よりも高くなります。

実際に使う場合には、この 2 つのうちではRidge回帰をまず試してみると良いでしょう。しかし、特徴量が多く、そのうち重要なものは僅かしかないことが予測されるのであれば、Lasso が適しています。
同様に、解釈しやすいモデルが適している際は、重要な特徴量のサブセットを選ぶLasso のが理解しやすいモデルが得られます。