もくじ

1. 因果推論とは何か
2. 交絡とは何か
3. 交絡の調整法
4. 因果推論の例
5. まとめ
6. 参考文献

1. 因果推論とは何か

因果推論とはある要因の間に因果関係があることを推論することである。因果推論をするための手法は多岐に渡るが、その前に因果関係について説明をしておく。

因果関係とは2つの要因が原因と結果という関係性で結びついていることである。これは原因となる要因が変化することで結果もまた変化する関係性にあることを示している。原因がA、結果がBであるとき、以下のような因果関係となる。

ここで注意しておきたいのが、相関関係と因果関係の違いである。相関関係は2つの変数がどちらか一方が大きければ、もう一方もまた大きい(または小さい)かどうかというデータの「あり方」について述べているのに対し、因果関係には原因となる変数と結果となる変数があり、それは「原因に対し介入を加えることで結果が変わる」ものを指す。

つまり、相関関係があるということだけでは因果関係があるとは言えず、またどちらの変数が原因なのか、あるいは結果なのかを説明する根拠にはなりえないのである。因果推論は先に述べた相関と因果の取り違いのような因果関係の誤謬に注意して原因と結果を推論する行いだと言える。

2. 交絡とは何か

因果推論を説明する上で重要になってくるのが交絡である。交絡とは以下のような因果の構造を指す。

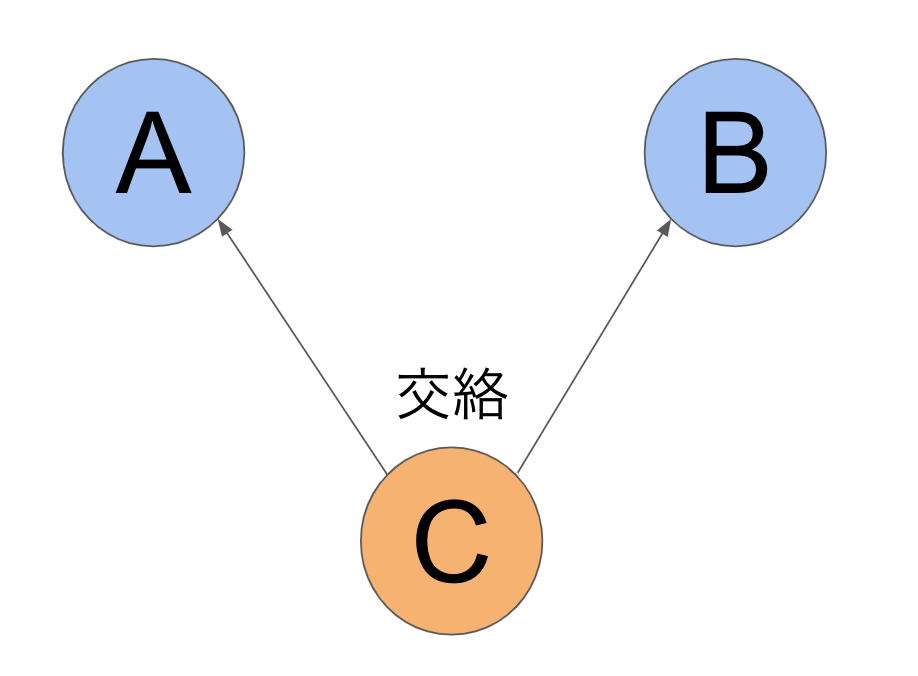
上のような2つの要因の両方に影響するものを交絡因子と呼ぶ。この交絡因子Cが要因AとBの両方に影響することで、あたかもAとBが因果関係を持っているように思えるのである。

因果関係を正しく推論するためには、この交絡に対処する必要がある。観察されたデータに相関関係がみられるとき、それが因果関係によるものなのかあるいは交絡因子の影響によるものなのかを何かしらの方法によって区別しなければならない。

そのために交絡因子の調整を行い、その影響によって差が生じることを防ぐ必要がある。これは交絡因子の影響を固定し変化しないようにすることで、原因と結果だと思われる要因の関係を検討することである。3節では実際に行われる交絡の調整法について述べる。

3. 交絡の調整法

交絡の調整には様々な手法が存在するが、ここではその中でも広く使われているランダム化比較試験と層別解析の2つの手法について説明する。

ランダム化比較試験(RCT)

ランダム化比較実験(randomized controlled trial, 以下RCTと呼ぶ)とは原因と考えられる要因を変化させながらその結果の変化を見ていく中で、その結果の差を見るために介入を行うかどうかを無作為に行うことである。

具体例を挙げて示そう。ある医薬品Aを服用するかどうかによってその対象者の血糖値Bが下がるかどうかを考える。このとき、医薬品Aを服用するかどうかは無作為に決められなければならない。より詳しく言うならば、医薬品Aを服用するグループと服用しないグループで、その他の要因の偏りが生じてしまってはいけないのである。このグループ間の偏りが交絡因子の影響によるものだと考えられ、交絡因子として実験を行うときに知っている要因もあれば、全く知らない未知の要因も存在する。

しかし、このRCTを行い無作為に対象者を選ぶことで、既知の要因も未知の要因も2つのグループ間で平均的に同じぐらいにすることができる。つまり、交絡因子による影響を同程度にしながら医薬品Aの効果、つまり血糖値Bが低下するかどうかという因果関係を知ることができるのである。

層別解析

実験研究においてはRCTは可能であったが、介入の無作為化が困難な場合がある。例えば喫煙者と非喫煙者との間で喫煙の有無による影響を測定するときに、対象者ごとに喫煙するかどうかを実験をする者が決めることはできない。そうした際に、喫煙者と非喫煙者のそれぞれの特徴には偏りが生じると考えられる。

このようなデータに対する手法として層別解析が挙げられる。層別解析とは交絡因子として考えられる特徴について、その特徴が同じ水準のサンプルごとに層として分けて解析を行うことである。これにより、分けられた層の中では特徴が似通っている、つまり交絡因子の影響が同程度になるので正しい推論が可能となる。

この他にもマッチングや回帰モデルを用いた分析、傾向スコアを用いた分析などが存在し、それぞれ交絡因子の影響を調整する手法として広く使われている。

4. 因果推論の例

現在、因果推論は経済学や社会科学、心理学や臨床医学など多岐に渡る分野で応用されている。この節ではそんな因果推論の利用を身近な例からいくつか紹介したいと思う。

偶然の関係

「ニコラス・ケイジの1年間の映画出演回数」と「同年の水泳プールでの溺死者数」には相関関係があるという結果が示されている。しかし、常識的に考えればこの2つの要因には因果関係はない。このようなあからさまな例では誰しもが因果関係は無いことに気づくが、相関関係のあるデータには常にこの問題がつきまとう。

擬似的な相関関係を見て要因間のありもしない因果関係を「でっちあげ」ていることが、我々の生活の中で行われていることが意外にも多いのである。このような間違いを回避するためにも、因果推論の考え方は重要である。

交絡因子による影響

「子供の体力」と「子供の学力」に相関があるというとき、どのように結論づけるべきだろうか？体力と学力の間には因果関係はあるといえるのか？

前の節でも述べたように、2つの要因の相関性が別の交絡因子によるものであることがある。今回の場合、「親の教育への関心の高さ」を考えるとどうだろうか。教育に関心の高い親は、子供の体力作りに熱心であると同時に、学力向上にも力を入れていることが多いであろう。

つまり、「親の教育への関心の高さ」が交絡因子となり「子供の体力」と「子供の学力」に影響して相関関係が現れていると考えられる。因果推論する上で交絡を見つけ出すことも重要となる。

因果の向き

因果推論をする際には、因果関係があるということが言うだけでなく、その向きについても正しく推論するべきである。「アイスクリームが売れる」から「気温が高い」のではなく、「気温が高い」から「アイスクリームが売れる」と考えるのが自然である。

ただデータを見るだけではどちらの要因が原因で、どちらの要因が結果になるのかという「因果の向き」の推論を行うことは難しい。要因間の関係を慎重に解析し、因果の向きを取り違えないように推論する必要がある。

5. まとめ

今回の記事では、以下の事柄について述べた。

• 因果推論について
• 交絡とその調整法について
• 実生活の中での因果推論の例

因果推論の手法には、まだまだ紹介しきれていないものもある。また、データから正しい推論をするデータサイエンスの領域では、今後も因果推論の考え方は重宝されていき、より発展していく分野だといえる。

6. 参考文献

• 中室 牧子, 津川 友介『「原因と結果」の経済学―――データから真実を見抜く思考法』, ダイヤモンド社, 2017
• 岡本 厚『岩波データサイエンス Vol.3 特集 因果推論―　実世界のデータから因果を読む』, 岩波書店, 2017
• 星野 崇宏『確率と情報の科学 調査観察データの統計科学　因果推論・選択バイアス・データ融合』, 岩波書店, 2017

Twitter・Facebookで定期的に情報発信しています！
Follow @acceluniverse